Q) A man on a cliff observes a boat at an angle of depression of 30° which is approaching the shore to the point immediately beneath the observer with a uniform speed. Six minutes later, the angle of depression of the boat is found to be 60°. Find the time taken by the boat from here to reach the shore.

Ans: Let’s start with the diagram for this question:

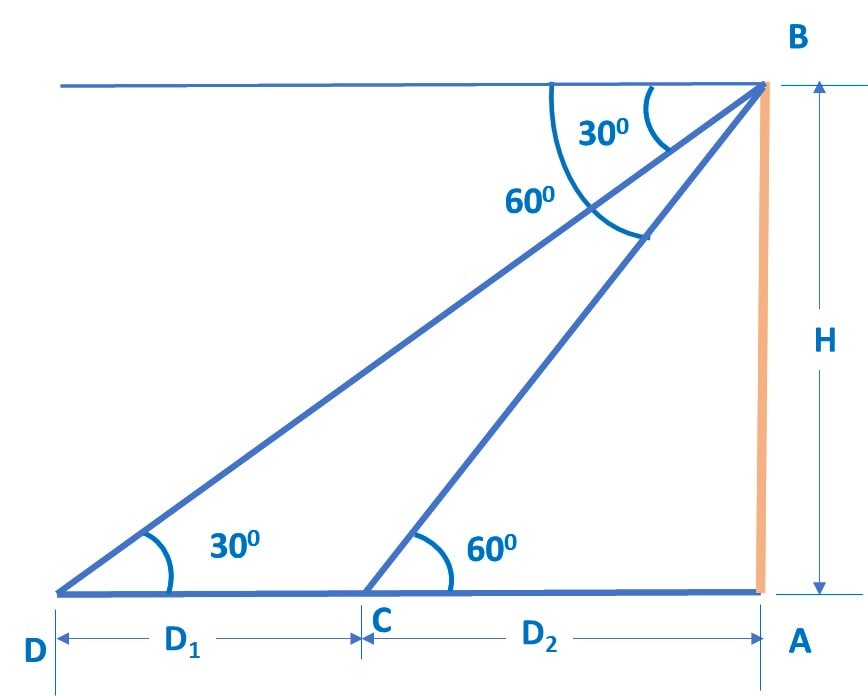
Here, let’s consider AB is the cliff and the boat initially at point D, and then after 6 minutes, it is at point C.

Given that the angle of depression from point B at the Tower top to the boat at Point D is 30⁰, the elevation angle from D to point B will be 30⁰.

Similarly, since the angle of depression from point B at the Tower top to the boat at Point C is 60⁰, the elevation angle from C to point B will be 60⁰.

Let’s consider the distance covered by the boat from point D to point C is D₁ and the distance from C to point A at the foot of the tower is D₂.

Step 2: Find the distance D₁:

In Δ ABD,

tan 30 =

∴

∴ AD = H√ 3….. (i)

Similarly, in Δ ABC,

tan 60 =

∴ √ 3 =

∴ D₂ = ….. (ii)

We can see that CD = AD – AC or D₁ = AD – D₂

Substituting the values from equations (i) and (ii), we get

D₁ = H √3 –

∴ D₁ = H(√3 – )

∴ D₁ = H()

∴ D₁ =

Step 3: Find the speed of the boat

Now, it is given that this distance is covered in 6 minutes

We know that: Speed =

∴ Speed =

∴ Speed =

Step 4: Find the time taken to cover CA

Now the boat will cover distance D₂ with the speed of

We know that: Speed =

∴ Time =

Substituting the values of distance and speed, we get

Time =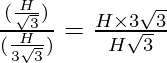

∴ Time =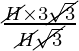

∴ Time = 3 minutes

Therefore, the distance from point C to point A will be covered in 3 minutes.

Please press the “Heart” button if you like the solution.