Q) ABCD is a parallelogram. P is a point on side BC and DP when produced meets AB produced at L. Prove that:

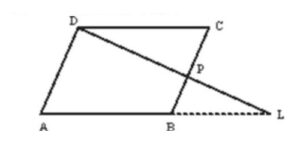
(i)

(ii)

(iii) If LP : PD = 2 : 3, then find BP : BC

Ans: (i) Solution for :

Step 1: Since DC ǁ AB (and hence AL)

and Line CB cuts these parallel lines,

Therefore, ∠ DCB  = ∠ CBL

∴ ∠ DCP = ∠ PBL ……… (i)

Step 2: Similarly, Line DL cuts the parallel lines CD and AL,

Therefore, ∠ CDL  = ∠ ALD

∴ ∠ CDP = ∠ BLP …. (ii)

Step 3: Let’s compare Δ DCP with Δ PBL

We have ∠ DCP = ∠ PBL    [from equation (i) ]

and ∠ CDP = ∠ BLP .          [from equation (ii) ]

Therefore, by AA similarity rule,

∴ Δ DCP ~ Δ PBL

∴   

(ii) Solution for

Step 1: Line DL cuts the parallel lines CD and AL,

Therefore, ∠ CDL  = ∠ ALD

∴ ∠ CDP = ∠ ALD (interior angles) …..  (i)

Step 2: Since ABCD is a parallelogram,

Therefore, ∠ DAB  = ∠ DCP   (Opposite angles)…..(ii)

Step 3: Let’s compare Δ DAL with Δ DCP

We have ∠ CDP = ∠ ALD    [from equation (i) ]

and ∠ DAB = ∠ DCP .          [from equation (ii) ]

Therefore, by AA similarity rule,

∴ Δ DAL ~ Δ DCP

∴

(iii)   Solution for BP : BC:

Since Δ DCP ~ Δ PBL

Given that =

∴

∴ PC = BP

Since BC = BP + BC

∴ BC = BP + BP

∴ BC = BP (1 + )

∴ BC = BP

Please press Heart if you liked the solution.