Q) AD and PS are medians of triangles ABC and PQR respectively such that Δ ABD ~ Δ PQS. Prove that Δ ABC ~ Δ PQR.

PYQ: Q 24 – CBSE 2025 – Code 30 – Series 5 – Set 1

Ans:

Step 1: Let’s first draw a diagram for the given question:

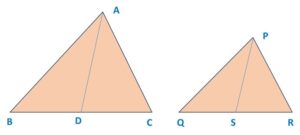
[Note: prefer to draw a diagram for a question, it makes the question clear and chances of error get removed completely]

Step 2: It is given that: ΔABD ∼ ΔPQS

∴ AB / PQ = BD / QS = AD / PS

and ∠ B = ∠ Q

Step 3: It is given that AD and PS are the medians of the triangles Δ ABC and Δ PQR respectively

∴ D is the midpoint of BC and S is the midpoint of QR

∴ BD = BC / 2 and QS = QR / 2

Step 4: Substituting these values in the above equation in step 2, we get:

∴ AB / PQ = (BC / 2) / (QR / 2)

∴ AB/ PQ = BC / QR

Also we have ∠ B = ∠ Q  (from step 2 above)

∴  By applying Side-Angle-Side (SAS) criterion for similarity of triangles, we get:

Δ ABC ∼ Δ PQR ………… Hence Proved!

Please press the “Heart” button if you like the solution.