Q) From a solid cylinder of height 24 cm and radius 5 cm, two cones of height 12 cm and radius 5 cm are hollowed out. Find the volume and surface area of the remaining solid.

PYQ: 34 (b) – CBSE 2025 – Code 30 – Series 5 – Set 1

Ans: 

Given that the height of the cylinder, H_cyl = 24 cm

radius of the cylinder, R_cyl = 5 cm

height of the cone, H_cone = 12 cm

and radius of the cone, R_cone = radius of the cylinder, R_cyl = 5 cm

Let’s draw the diagram to capture the shape:

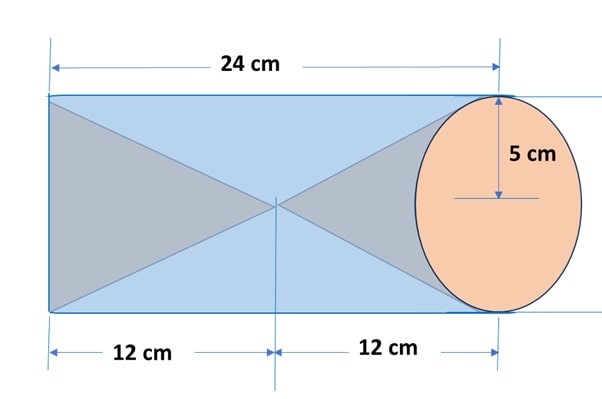
Part 1: Volume of the remaining solid:

Total Volume of the remaining solid after hollowing out = Volume of the cylinder – 2 (volume of conical cavities) ………… (ii)

Let’s calculate each part of the equation one by one:

a) Volume of the cylinder  = π R_cyl ² H_cyl

= π x (5) ² (24) = 600 π cm³

b) Volume of the cone = (1/3) π R_cone ² H_cone

= (1/3) π (5)² (12) = 100 π cm ³

c) By substituting these values in equation (ii), we get:

Total Volume of the remaining solid after hollowing out = Volume of the cylinder – 2 (volume of conical cavities) ………… (ii)

= 300 π – 2 (100 π) = 100 π

= 100 x (22 / 7) = 314.29 cm³

Therefore, the volume the remaining solid is 314.29 cm³.

Part 2: Total surface area of the remaining solid: 

Total surface area of the remaining solid after hollowing out = curved surface area of the cylinder + 2 (curved surface area of the cone) ……(i)

(When cones are hollowed out from the cylinder, base is removed, but curved surface area of the conical shape gets added on either side)

Let’s calculate each part of the equation one by one:

a) Curved surface area of the cylinder  = 2 π R_cyl H_cyl

= 2 π x 5 x 24 = 240 π cm²

b) Curved surface area of the cone = π R_cone L_cone

= π (5) [√(5 ² + 12 ²)]

= π (5) (13)        (Important: remember, 5, 12, 13 are one of the triplets)

= 65 π cm

c) By substituting these values in equation (i), we get:

Total surface area of the remaining solid after hollowing out = curved surface area of the cylinder + 2 (curved surface area of the cone) ……(i)

= 240 π + 65 π = 305 π

= 305  x (22 / 7) = 958.71 cm²

Therefore, the total surface area of the remaining solid is 958.71 cm².

Please press the “Heart”, if you like the solution.