Q) From one of the faces of a solid wooden cube of side 14 cm, maximum number of hemispheres of diameter 1.4 cm are scooped out. Find the total number of hemispheres that can be scooped out. Also, find the total surface area of the remaining solid.

PYQ: 34 (a) – CBSE 2025 – Code 30 – Series 5 – Set 1

Ans: 

Given: Side of the cube = 14 cm

and Diameter of the hemisphere = 1.4 cm

∴ Radius of the hemisphere = 1.4 / 2 = 0.7 cm

Part 1: Total number of hemispheres:

Step 1: Let’s start with a diagram for the hemispheres scooped on a surface:

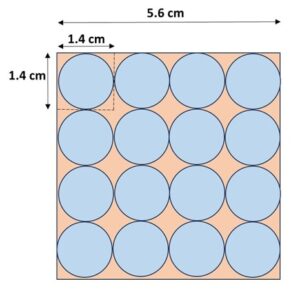
Here the hemispheres are being scooped out from the top face. Let’s understand the number of hemispheres carefully:

When a circular shape will be scooped out from a face, it will take a space equal to its diameter in all directions. Here, width of the circular base of scoop will decide how many such hemispheres can be taken out from the face. Note, the depth of the hemisphere has nothing to do with the face’s area.

Let’s understand by an example:

Since diameter of the hemisphere is 1.4 cm, hence, a hemisphere will acquire minimum space of a square of size 1.4 cm x 1.4 cm (the minimum length and breadth of the square can not be less than 1.4 cm)

For ease of understanding, let’s assume we take 4 such hemisphere adjacent to each other, they would take 4 x 1.4 cm = 5.6 cm along the length

Similarly 2nd row will get 4 such squares, 3rd row will get 4 such squares and 4th row will also get 4 such squares.

Hence, maximum 16 squares will come in a square space of 5.6 x 5.6.

or we can say, 5.6 x 5.6 square space will accommodate 16 squares of 1.4 cm x 1.4 cm

Similarly, Number of hemisphere possible to be scooped out from the top face of 14 cm x 14 cm size

= Area of the face / Area taken by one hemisphere

= (14 x 14) / (1.4 x 1.4)

= 10 x 10 = 100 numbers

Therefore, Total 100 hemisphere can be scooped out from one face of the cube.

(Note: Dividing by hemisphere’s curved surface area will be wrong as depth of hemisphere has nothing to do with 2D shape of top face)

Part 2: Surface area of the remaining solid:

Step 2: Let’s make a diagram of the resulting body: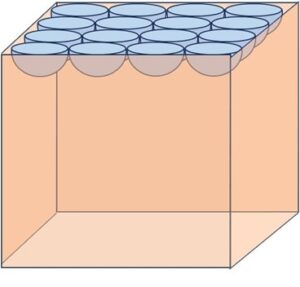

We can see that the Total surface area of the remaining solid can be given by:

Total surface area = Surface area of the top face + Surface area of other 5 faces…………. (i)

Let’s calculated all of these one by one:

Step 3: Surface area of the top face:

= Surface area of 100 hemispheres + Surface area of the top face remained after scooping out hemispheres

= Surface area of 100 hemispheres + (Surface area of the original top face – circular area of 100 hemispheres) ………. (ii)

Step 4: Since Surface area of a hemisphere is given by 2 π r ²

∴ Surface area of 100 hemispheres = 100 x 2 π r ² = 200 π r ²

here, radius of the hemisphere = 0.7 cm

∴ Surface area of 100 hemispheres = 200 x (22 / 7) x (0.7) ²

= 200 x 22 x 0.1 x 0.7 cm ²

= 44 x 7 = 308 cm ²

Step 5: Surface area of the original top face

= (Side of the cube) ²

= (14) ² = 196 cm ²

Step 6: Circular area of 100 hemispheres = 100 x π r ²

here, radius of the hemisphere = 0.7 cm

∴ circular area of 100 hemispheres = 100 x (22 / 7) x (0.7)²

= 100 x 22 x 0.1 x 0.7

= 22 x 7 = 154 cm²

Step 7: By substituting all these 3 values in the equation (ii), we get:

Surface area of the top face = Surface area of 100 hemispheres + (Surface area of the original top face – circular area of 100 hemispheres)

= 308 + (196 – 154)

= 308 + 42 = 350 cm²

Step 8: Next, let’s put this value in the equation (i):

Total surface area of the remaining solid = Surface area of the top face + Surface area of other 5 faces

= 350 + 5 (14 x 14)

= 350 + 980 = 1330 cm²

Therefore, Total surface area of the remaining solid is 1330 cm²

Please press the “Heart”, if you like the solution.