Q) Passenger boarding stairs, sometimes referred to as boarding ramps, stair cars or aircraft steps, provide a mobile means to travel between the aircraft doors and the ground. Larger aircraft have door stills 5 to 20 feet (1 foot = 30 cm) high. Stairs facilitate safe boarding and de-boarding.

An aircraft has a door sill at a height of 15 feet above the ground. A stair car is placed at a horizontal distance of 15 feet from the plane.
Based on given information, answer the questions given in part (i) and (ii).
(i) Find the angle at which stairs are inclined to reach the door sill 15 feet high above the ground.
(ii) Find the length of stairs used to reach the door sill.
Further, answer any one of the following questions:
(iii) If the 20 feet long stairs is inclined at an angle of 60 deg to reach the door sill, then find the height of the door sill above the ground. (use √3 = 1.732)
(iv) What should be the shortest possible length of stairs to reach the door sill of the plane 20 feet above the ground, if the angle of elevation cannot exceed 30 deg ? Also, find the horizontal distance of base of stair car from the plane.

PYQ: 37 – CBSE 2025 – Code 30 – Series 5 – Set 1

Ans:

(i) Angle of stairs inclination:

Let’s start by making a diagram for our better understanding of the question: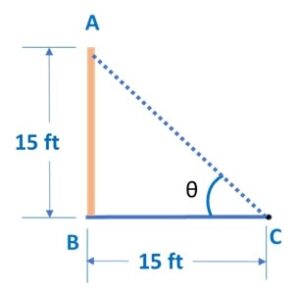

In the above diagram, Door sill is at Point A, which is 1 feet high from the ground B. Stair car is at point C which is 15 feet from the point B.

We need to find value of ∠ ACB – Let’s consider it as θ.

Now We start from Δ ABC, here since we have value of height as well as base, we can apply tan θ formula to get value of θ

∵ tan θ = AB / BC

∴ tan θ = 15 / 15 = 1

We know that for tan 45⁰ = 1

∴ tan θ = tan 45⁰

∴ θ = 45⁰

Therefore, angle of stairs inclination is 45⁰

(ii) Length of stairs to reach the door sill:

Let’s look at the diagram again:

Here, we already have Height AB = 15 feet, Base BC = 15 feet, Angle θ = 45⁰, and now length of the stairs, AC, is to be calculated.

In Δ ABC, sin θ = AB / AC

∴ sin 45⁰ = 15 / AC

∴ 1 / √2 = 15 / AC

∴ AC = 15 √2 feet

Therefore, length of the stairs is 15 √2 feet.

(iii) Height of the door for 20 feet long stairs inclined at 60⁰:

Let’s start by making a diagram for our better understanding of the question: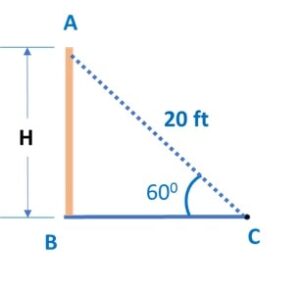

Here, AC is length of stairs given as 20 feet and angle of elevation is 600, We need to find the AB, height of door sill from ground.

Let’s consider the height is H feet

In Δ ABC, sin 60⁰ = AB / AC

∴ sin 60⁰ = H / 20

∴ √3 / 2 = H / 20

∴ H = 20 √3 /2 = 10 √3 feet

Given, √3 = 1.732, ∴ H = 10 x 1.732 = 17.32 feet

Therefore, height of the door sill in this case is 17.32 feet

(iv) Shortest possible length of stairs to reach the door and horizontal distance of base of stair car:

Let’s start by making a diagram for our better understanding of the question: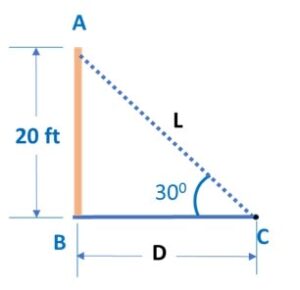

Passenger boarding stairs, sometimes referred to as boarding ramps, stair cars or aircraft steps,

Here, it is given, that height of door sill AB is 20 ft, maximum angle of elevation is 30⁰, and we need to find length of stairs L

In Δ ABC, sin θ = AB / AC

∴ sin 30⁰ = 20 / L

∴ 1 / 2 = 20 / L

∴ L = 20 x 2 = 40 feet

Therefore, the shortest possible length of the stairs is 40 feet.

At this stage, BC is the distance of stairs car from plane ground.

Let’s consider this distance is D feet

In Δ ABC, tan θ = AB / BC

∴ tan 30⁰ = 20 / D

∴ 1 / √3 = 20 / D

∴ D = 20 √3

By taking √3 = 1.732, we get D = 20 x 1.732 = 34.64 feet

Therefore, the horizontal distance of base of stair car from the plane is 34.64 feet.

Please press the “Heart” button if you like the solution.