Q) Show that the points (- 2, 3), (8, 3) and (6, 7) are the vertices of a right-angled triangle.

Ans: Let’s plot these points on graph, we get:

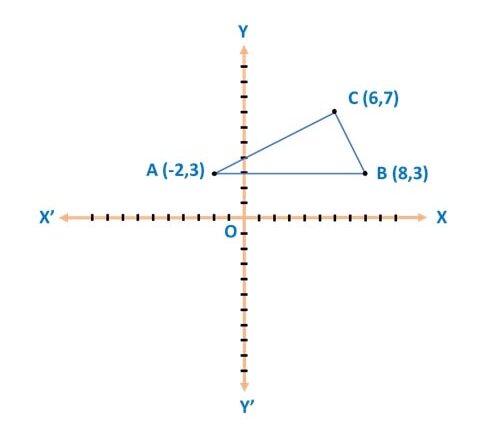
Step 1: Now for a Δ ABC to be an right angled triangle, required condition is:

AB² = AC² + BC²

Step 2: Let’s calculate the lengths of each of the three sides:

We know that the distance between two points (X₁, Y₁) and (X₂, Y₂) is given by:

S = √ (X₂ – X₁)² + (Y₂ – Y₁)² )

∴  AB = √ (8 – (- 2))²  + (3 – (3))² ) = √(10²  + 0) = 10 units

Similarly, BC = √ ((8 – 6)²  + (3 – 7)² ) = √ (4 + 16) = √ 20 units

Similarly, AC = √ (6 – (- 2))²  + (7 – 3)² ) = √ (64 + 16) = √80 units

Step 3: Since, (10) ²  = (√20) ²  + (√80) ²

Or AC² = AB²  + BC²

Therefore, triangle ABC is a right-angled triangle.

Please press the “Heart”, if you liked the solution.