Q) From a solid right circular cone, whose height is 6 cm and radius of base is 12 cm, a right circular cylindrical cavity of height 3 cm and radius 4 cm is hollowed out such that bases of cone and cylinder form concentric circles. Find the surface area of the remaining solid in terms of π.

Q34 A – Sample Question Paper – Set 1 – Maths Standard – CBSE 2026

Ans:

Note: Concentric means circles have same centre. Hence, we will take radius of the cone and cylinder around around same axis.

Let’s start by making a neat diagram for better understanding of the question:

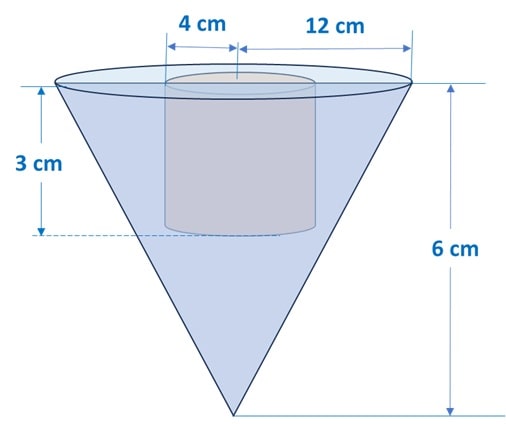
When a cylinder is cut from the cone’s base, the Curved surface area of remaining solid will be cumulative of following surface areas:

a) Curved surface area of the Cone

b) Base Area which will be net of Cone’s base area – Cylinder’s base area

c) Total surface area of Cylinder which will be sum of curved area of Cylinder + Cylinder’s base area (only 1 base is included, other base gets removed while hollowing out the solid)

Let’s calculate each of them one by one:

a) Curved surface area of the Cone:

Given that Radius of Cone, R_cone = 12 cm and Height of Cone, H_cone = 6 cm

∴ Slant height of the Cone, L_cone = √ [(12)² + (6)²] = √ (144 + 36) = √ 180 = 6√5 cm

Curved surface area of the Cone =  π R_cone L_cone  = π x 12 x 6 √ 5 = 72 √5 π cm²

b) Base Area:

Base area = Cone’s base area – Cylinder’s base area

= π R_cone² – π R_cyl²

= π x 12²  – π x 4²

= 144 π  – 16 π  = 128 π cm²

c) Total surface area of Cylinder = Curved area of Cylinder + Cylinder’s base area

= 2 π R_cyl H_cyl + π R_cyl²

= 2 π x 4 x 3 + π (4)²

= 24 π + 16 π  = 40 π cm²

d) ∵  Curved surface area of remaining solid = Curved surface area of the Cone + Base Area + Total surface area of Cylinder

= 72 √5 π + 128 π + 40 π = 168 π + 72 √5 π = (168 + 72 √5 ) π cm²

Therefore, the Surface area of the remaining solid is (168 + 72 √5 ) π cm²

Please do press “Heart” button if you liked the solution