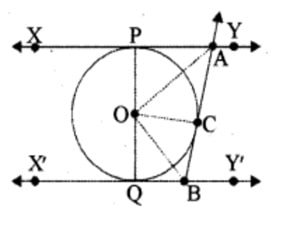
Q) In Figure, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°

Q26 A – Sample Question Paper – Set 1 – Maths Standard – CBSE 2026

Ans:

STEP BY STEP SOLUTION

Step 1: Let’s start comparing with Δ APO and Δ ACO:

From Point A, 2 tangents AP and AC are drawn,

∴  AP = AC   (tangents drawn from a points are equal)

OP = OC     (Being radii of same circle)

AO = AO     (common arm)

∴ Δ APO ≅ Δ  ACO

∴ ∠ POA = ∠ COA …………. (i)

Step 2: Next, let’s compare with Δ BQO and Δ BCO:

From Point B, 2 tangents BQ and BC are drawn,

∴  BQ = BC   (tangents drawn from a points are equal)

OQ = OC     (Being radii of same circle)

BO = BO     (common arm)

∴ Δ BQO ≅ Δ  BCO

∴ ∠ QOB = ∠ COB ……….. (ii)

Step 3: At Point O, we can see that there are 4 angles are formed and sum of all 4 angles is 180⁰

∴ ∠ POA + ∠ COA + ∠ COB + ∠ QOB = 180⁰

from equation (i), we have ∠ POA = ∠ COA and from equation (ii), we have ∠ QOB = ∠ COB

∴ (∠ COA) + ∠ COA + ∠ COB + (∠ COB) = 180⁰

∴ 2 (∠ COA + ∠ COB) = 180⁰

∴ ∠ COA + ∠ COB = 90⁰

∵ ∠ COA + ∠ COB = ∠ AOB      (from the diagram)

∴ ∠ AOB = 90⁰       ………… Hence Proved !

Please press the “Heart” button if you like the solution.