Q) The discus throw is an event in which an athlete attempts to throw a discus. The athlete spins anti-clockwise around one and a half times through a circle, then releases the throw. When released, the discus travels along tangent to the circular spin orbit.

In the given figure, AB is one such tangent to a circle of radius 75 cm. Point O is centre of the circle and ZABO =30″. PQ is parallel to OA.
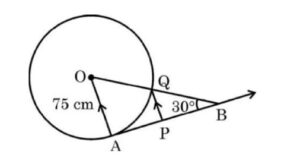
Based on above information:
(a) find the length of AB.
(b) find the length of OB.
(c) find the length of AP.
OR
Find the length of PQ
Ans:
VIDEO SOLUTION
STEP BY STEP SOLUTION
(i) Value of line AB:
In ΔOAB, tan 30° = ![]()
![]() =
= ![]()
AB = 75√3 cm
(ii) Value of line OB:
In ΔOAB, Sin 30° = ![]()
![]() =
= ![]()
OB = 75 x 2
OB = 150 cm
(iii) Value of line AP:
Now, given that radius OA = OQ = 75 cm
therefore, QB = OB – OQ = 150 -75 = 75 cm
Therefore, Q is midpoint of line OB
Given that PQ ǁ AO, and since, we just found that Q is midpoint of line OB,
Therefore, P is midpoint of AB.
Hence AP = ![]() =
= ![]()
AP = ![]() cm
cm
OR
Value of line PQ:
Method 1:
We have just found out that OQ = QB = 75 cm
Now, In ΔQPB, Sin 30° = ![]()
![]() =
= ![]()
PQ = ![]() =
= ![]()
PQ = ![]() cm
cm
Method 2:
In ΔOAB and ΔQPB
OQ = QB, AP = PB, ∠OBA = ∠QBP
Therefore, ΔOAB ~ ΔQPB
![]() =
= ![]()
![]() =
= ![]()
PQ = ![]() cm
cm
