Q) Two tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠ APB= 2 ∠ OAB.

(Q26 B – Sample Question Paper – CBSE 2026)

OR

Q) Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠ PTQ = 2 ∠ OPQ

(Q 29 B – 30/2/1 – CBSE 2026 Question Paper)

Ans:

Step 1: Let’s make a diagram for better understanding of the question:

(Further, we can solve by 2 methods. For your ease, I have solved by both methods, you can choose and adopt any one method, whichever you find easier)

Method 1:

Step 2: In Δ OAB, OA and OB are radii of same circle

and angles opposite to equal sides are equal

∴ ∠ OAB = ∠ OBA ……….. (i)

Step 3:  ∵ By angle -sum property, the sum of all angles in a triangle is 180.

∴ In Δ OAB,  ∠ OAB + ∠ OBA + ∠ AOB = 180 ⁰

∵ ∠ OAB = ∠ OBA               (from equation (i))

∴ ∠ OAB + ∠ OAB + ∠ AOB = 180 ⁰

∴ 2 ∠ OAB + ∠ AOB = 180 ⁰    ………… (ii)

Step 4: Since OAPB is a cyclic quadrilateral,

∠ AOB + ∠ OAP + ∠ APB + ∠ OBP = 360 ⁰   

∵ ∠ OAP = ∠ OBP =  90 ⁰              (Radius is Ʇ to tangent)

∴ ∠ AOB + 90 ⁰  + ∠ APB + 90 ⁰  = 360 ⁰   

∴ ∠ AOB + ∠ APB + 180 ⁰  = 360 ⁰   

∴ ∠ AOB + ∠ APB =  360 ⁰ – 180 ⁰    = 180 ⁰ ………… (iii)

Step 5: By comparing equation (ii) and equation (iii), we get:

∠ AOB + ∠ APB = 2 ∠ OAB + ∠ AOB

∴ ∠ APB = 2 ∠ OAB ………….  Hence Proved !

Therefore, it is proved that ∠ APB = 2 ∠ OAB

Method 2:

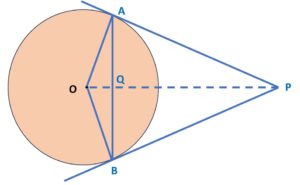
Step 2: Next, we compare Δ OAQ and Δ OBQ:

Since OA and OB are radii of same circle,

∴ OA = OB

AQ = BQ        (since OP is perpendicular bisector to AB)

OQ = OQ       (being common arm)

∴ by SSS criterion, Δ OAQ ≅ Δ OBQ

∴ ∠ OAQ = ∠ OBQ              (by CPCT) …………(i)

Step 3: Next, we take Δ OAP:

In Δ OAP,  ∠ OAP + ∠ APO + ∠ POA = 180 ⁰

∴ 90 ⁰ + ∠ APO + ∠ POA = 180 ⁰

(∵ tangent drawn on a circle is perpendicular to radius)

∴ ∠ APO + ∠ POA = 180 ⁰ – 90 ⁰

∴ ∠ APO + ∠ POA = 90 ⁰   ………………. (ii)

Step 4: In Δ OAQ,  ∠ OAQ + ∠ AQO + ∠ QOA = 180 ⁰

∴ ∠ OAQ + 90 ⁰ + ∠ QOA = 180 ⁰     (since cord AB is perpendicular to OP)

∴ ∠ OAQ + ∠ QOA = 180 ⁰ – 90 ⁰

∴ ∠ OAQ + ∠ QOA = 90 ⁰ ………………. (iii)

Step 5: By comparing equation (ii) and equation (iii), we get:

∠ APO + ∠ POA = ∠ OAQ + ∠ QOA

∵ ∠ POA and ∠ QOA are name of same angles

∴ ∠ APO = ∠ OAQ   …………. (iv)

Similarly, we can prove that ∠ BPO = ∠ OBQ  ………….. (v)

Step 6: By adding equations (iv) and equation (v), we get:

∠ APO + ∠ BPO = ∠ OAQ + ∠ OBQ

∴ ∠ APB = ∠ OAQ + ∠ OBQ

From equation (i), we have ∠ OAQ = ∠ OBQ

∴ ∠ APB = 2 ∠ OAQ

∵ ∠ OAQ and ∠ OAB are name of same angles

∴ ∠ APB = 2 ∠ OAB  ………. Hence Proved !

Therefore, it is proved that ∠ APB = 2 ∠ OAB

Please press the “Heart” button if you like the solution.