Q) A group of class X students goes to picnic during winter holidays. The position of three friends Aman, Kirti and Chahat are shown by the points P, Q and R.

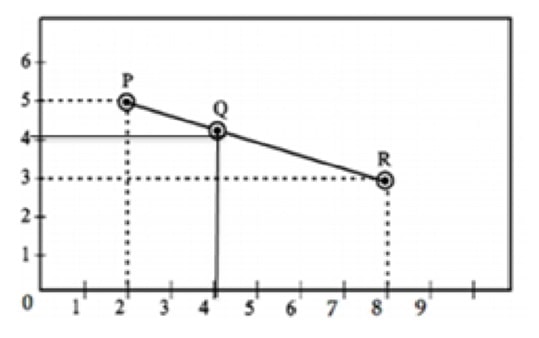
i. Find the distance between P and R.
ii. Is Q, the midpoint of PR? Justify by finding midpoint of PR.
iii. Find the point on x-axis which is equidistant from P and Q.
iv. Let S be a point which divides the line joining PQ in ratio 2:3. Find the coordinates of S.

Q37 – Sample Question Paper – Set 1 – Maths Standard – CBSE 2026

Ans:

From the diagram, we can see that the coordinates of point P, Q and R are P (2, 5), Q (4, 4) and R (8,3) respectively.

i. Distance between P & R:

We know that the distance between two points A (X₁, Y₁) and B (X₂, Y₂) is given by:

AB = √ [(X₂ – X₁)² + (Y₂ – Y₁)² ]

Since we have coordinates of P & R as P (2, 5) and R (8, 3):

∴ Distance PR = √ [(8 – 2)² + (3 – 5)² ] 

∴ PR = √ (36 + 4) = √ 40  = 2 √10

Therefore, the distance between PR is 2 √10  units.

ii. Check if Q is the midpoint of PR:

We know that the co-ordinates of midpoint of 2 coordinates (X₁, Y₁) and (X₂, Y₂) given by:

(X, Y) = ( (X₁ + X₂) / 2, + (Y₁ + Y₂) / 2)

Here, we have co-ordinates of point P (2, 5) and Point R (8, 3)

∴ Co-ordinates of midpoint of P & R = ( (2 + 8) / 2, + (5 + 3) / 2) 

 = (5, 4)

From the diagram, we noted that coordinates of point Q are (4, 4).

The coordinates of these two points do not same.

Therefore, Q is not the midpoint of P & R.

iii. Coordinates of point on X – axis equidistant from P and Q:

Let’s consider a point S (x, y).

Since it is given that it lies on x – axis and we know that on x – axis, ordinate values are always 0,

hence coordinate of this point S will be (x, 0).

Next, if we calculate value of x, we will find the coordinates of the point S.

Since we are given that P and Q are equidistant from S, hence, we will calculate distance of each point from S and compare.

We will calculate PS and QS and compare.

We know that the distance between two points A (X₁, Y₁) and B (X₂, Y₂) is given by:

AB = √ [(X₂ – X₁)² + (Y₂ – Y₁)² ]

For PS, we have coordinates of P & S as P (2, 5) and S (x,0):

∴ Distance PS = √ [(x – 2)² + (0 – 5)² ] 

∴ PS = √ (x² – 4 x + 4 + 25) = √ (x² – 4 x + 29)   ……….. (i)

Next for QS, we have coordinates of Q & S as Q (4, 4) and S (x,0):

∴ Distance QS = √ [(x – 4)² + (0 – 4)² ] 

∴ QS = √ (x² – 8 x +16 + 16) = √ (x² – 8 x + 32)   ……….. (ii)

Since S is equidistant from P and Q both,

∴ PS = QS

∴ √ (x² – 4 x + 29)   = √ (x² – 8 x + 32)   

∴  (x² – 4 x + 29)   = (x² – 8 x + 32)   

∴  (- 4 x + 29)   = (- 8 x + 32)   

∴  8 x – 4 x  = 32 – 29

∴  4 x  = 3

∴  x = 3 / 4

∴  Coordinates of this point S will be (3 / 4, 0).

Therefore, point (3 / 4, 0) is the point on x-axis which is equidistant from P and Q.

iv. Coordinates of point S, divides the line PQ in ratio 2:3:

We know that according to Section formula, if a point A (x, y) divides the line segment joining the points A(x₁, y₁) and B(x₂, y₂) in the ratio m : n, then the coordinates of A are given by:  [ (m x₂ + n x₁) / (m + n), (m y₂ + n y₁) / (m + n) ]

Here we have, points P (2, 5) and point Q (4, 4) are the given points,

Let’s consider coordinates of point S as (x, y) which divides PQ in the ratio 2:3.

∴ x₁ = 2, y₁ = 5, x₂ = 4, y₂ = 4, m = 2, and n = 3

Let’s substitute these values into the section formula, we get coordinates of point S as:

x = (m x₂ + n x₁) / (m + n) = ( 2 x 4 + 3 x 2) / (2 + 3) = (8 + 6) / 5 = 14 / 5

y = (m y₂ + n y₁) / (m + n) = ( 2 x 4 + 3 x 5) / (2 + 3) = (8 + 15) / 5 = 23 / 5

Therefore the coordinates of point S are (14 / 5 , 23 / 5).

Please do press “Heart” button if you liked the solution