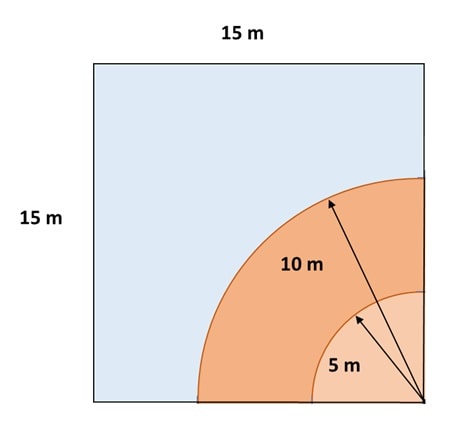
Q) A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope. Find the area of that part of the field in which the horse can graze. Also, find the increase in grazing area if length of rope is increased to 10 m. (Use л = 3.14)

Ans: Let’s draw a diagram and plot the given information.

(Note: your question will become clearer and your answer will never be wrong if you draw a diagram)

We know that the area a quarter of a circle of radius r is given by

From above diagram, area grazed by horse with 5m rope will be quarter of a 5 m radius circle =  = (3.14) (5)² = 19.625 m²

Therefore, with 5m rope, grazed area by horse will be 19.625 m² .

When rope length is increased to 10 m, the radius of the circle will be increased to 10 m and hence, the area grazed by horse will be quarter of a 10 m radius circle =

= (3.14) (10)² = 78.5 m² 

increased area  = 78.5 – 19.625 = 58.875 m²

Therefore, increase in the grazed area will be 58.875 m² .