Q) A hot air balloon is rising vertically from a point A on the ground which is at distance of 100m from a car parked at a point P on the ground. Amar, who is riding the balloon, observes that it took him 15 seconds to reach a point B which he estimated to be equal to the horizontal distance of his starting point from the car parked at P.

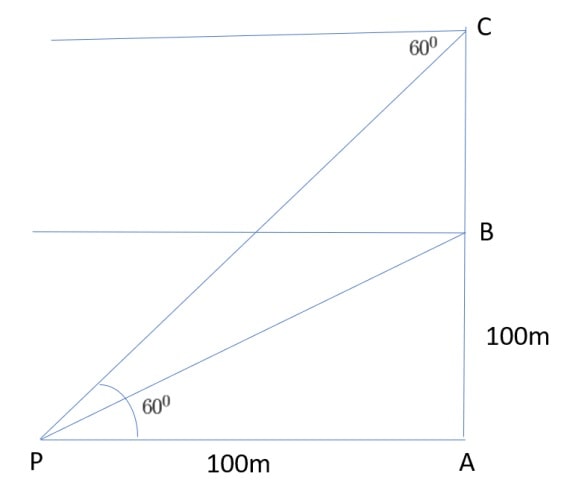
i. Find the angle of depression from the balloon at a point B to the car at point P.
ii. Find the speed of the balloon?
OR
ii. Find the total time taken by the balloon to reach the point C from ground?
iii. After certain time Amar observes that the angle of depression is 60. Find the vertical distance travelled by the balloon during this time

Ans:

VIDEO SOLUTION

 

STEP BY STEP SOLUTION

(i) Angle of Depression to point P from point B:

Angle of depression = ∠ BPA

In Δ BAP, tan θ = = 1

Since we know that tan 45° = 1,

∴  θ = 45°

Therefore, the Angle of Depression to point P from Point B is 45°.

(ii) Calculate the speed of the balloon:

Since we know that the speed =

Therefore, the speed = = 6.67 m/sec

Therefore, the speed of the balloon = 6.67 m/sec

(iii) Total time taken by the balloon to reach point C from the ground:

To get time, let’s first calculate the distance CA travelled by balloon:

In Δ CAP, tan 60 =

∴ √3  =

∴ CA = 100 √3 m

Now, since it is given that the balloon travelled 100 m in 15 sec (from ground to point B),

∴ it will travel 100 √3 m in = 15 √3

Therefore, the total time taken by the balloon to reach point C from the ground will be 15 √3 seconds

(iv) Vertical distance travelled by the balloon during this time:

After a certain time means observer’s location is changing from point B to point C and we need to calculate distance BC.

We just calculated in part (ii), that distance AC = 100√3 m

Therefore distance BC = AC – AB = 100√3 – 100 = 100 (√3 -1) m

Please do press “Heart” button if you liked the solution.