Q) In the given figure, AB and CD are tangents to a circle centred at O. Is angle BAC = angle DCA ? Justify your answer.

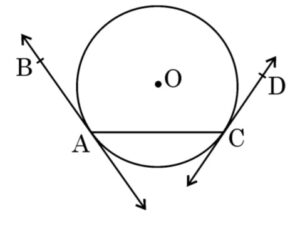
Ans: 

Step 1: Let’s connect center O with points A and C

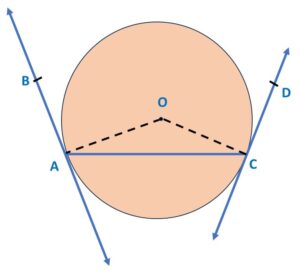
Step 2: Since BA is the tangent to the circle and OA is the radius of the circle,

∴ ∠ OAB = 90

Similarly, DC is the tangent to the circle and OC is the radius of the circle,

∴ ∠ OCD = 90

Step 3: Next, we look at Δ OAC:

Since OA and OC are radii of the circle

∴ the angles opposite to the equal sides are always equal

∴ ∠ OAC = ∠ OCA

Step 4: Next, we look in Δ OAC

∠ BAC = ∠ OAB + ∠ OAC

= ∠ OCD + ∠ OCA

= ∠ DCA

∴ ∠ BAC  = ∠ DCA

Hence Proved !

Please do press “Heart” button if you liked the solution.