If AD and PM are medians of triangle ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that AB / PQ = AD / PM.

Question

Q) If AD and PM are medians of triangle ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that AB / PQ = AD / PM.

Sapling Academy · Accepted Answer

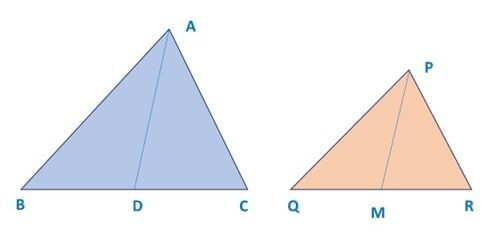
Step 1: Given that,  Δ ABC ~ Δ PQR, therefore

∠ B = ∠ Q   ............. (i)

and $\frac{AB}{PQ} = \frac{BC}{QR}$ ............. (ii)

Step 2: Since AD is median of BC, hence BC = 2BD

Similarly, PM is median of QR, hence QR = 2QM

Let's substitute these 2 values in equation (ii), we get:

$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{2BD}{2QM}$

∴ $\frac{AB}{PQ} = \frac{BD}{QM}$ ........ (iii)

Step 3: Let's compare Δ ABD ~and Δ PQM

Here, $\frac{AB}{PQ} = \frac{BD}{QM}$    (already proven in step 2)

∠ B = ∠ Q                      (deducted in step 1)

∴ Δ ABD ~ Δ PQM        (by SAS similarity)

Therefore, $\frac{AB}{PQ} = \frac{AD}{PM}$

Hence proved.

Please press the “Heart” button if you like the solution.

Contact us