Q) Prove that the tangents drawn at the end points of a chord of a circle makes equal angles with the chord.

Ans:

Let’s start by making a diagram for the question:

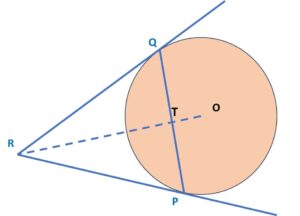
Here, we have circle with Centre O and PQ is a chord. From point R, two tangents are drawn at end points of chord, P and Q.

Next, we connect O with R and it intersects with PQ at point T.

Next, we know that, the line segment joining the centre of a circle to the external point, bisects the angle between two tangents.

∴ ∠ PRT = ∠ QRT …(i)

Next, let’s compare △ PRT with △ QRT, we have:

RP = RQ                      (Tangents on a circle from an external point)

∠ PRT = ∠ QRT           (from equation (i) above)

RT = RT                       (Common side)

∴ by SAS congruency rule: ∆ PRT ∆ DCB

Next, by applying CPCT theorem, we get:

∠ RPT = ∠ RQT

Hence Proved !

Please do press “Heart” button if you liked the solution.