Q) Radio towers are used for transmitting a range of communication services. including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure. On a similar concept, a radio station tower was built in two sections ‘A’ and ‘B’. Tower is supported by wires from a point ‘O’ (as shown in figure).
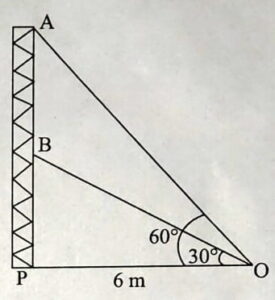
Distance between the base of the tower and point ‘O’ is 6 m. From point ‘O’, the angle of elevation of the top of the section ‘B’ is 30° and the angle of elevation of the top of section ‘A’ is 60°.
Based on the above information, answer the following questions:
(i) Find the length of the wire from the point ‘O’ to the top of section ‘B’.
(ii) Find the length of the wire from the point ‘O’ to the top of section ‘A’.
(iii) Find the distance AB.
(iv) Find the area of Δ OPB.
(Q 36 – 30/1/3 – CBSE 2026 Question Paper)
Ans:
Given PO = 6 m, ∠ BOP = 30°, ∠ AOP = 60°
(i) Length of the wire OB:
From the given diagram, we check in Δ BOP:
cos θ = cos 30° = 
∴ 
∴ BO = 
= 4√3 m
Therefore the length of wire OB is 4√3 m.
(ii) Length of the wire OA:
From the given diagram, we check in Δ AOP:
cos θ = cos 60° = 
∴ 
∴ AO = 12 m
Therefore the length of wire OA is 12 m.
(iii) Distance AB:
From the given diagram, AB = AP – BP
Step 1: In Δ AOP, tan 60° = 
∴ √3 = 
∴ AP = 6√3 m
Step 2: In Δ BOP, tan 30° = 
∴ 
∴ BP = 
= 2√3 m
Step 3: Length of AB = AP – BP
= 6√3 – 2√3
= 4√3 m
Therefore the length of AB is 4√3 m.
(iv) Area of Δ OPB:
∵ Area of a triangle is given by:
(base)(height)
∴ Area (Δ OPB) = (6)(2√3)
= 6√3 m2
Therefore, the area of Δ OPB is 6√3 m2
Please do press “Heart” button if you liked the solution.