Q) Solve the following system of equations graphically:

2x + y = 6

2 x – y – 2 = 0

Find the area of the triangle so formed by two lines and x axis

Q31 B – Sample Question Paper – Set 1 – Maths Standard – CBSE 2026

Ans:

Part 1: Solving the linear equations:

Step 1: To plot the equations, let’s first find out the coordinates of points lying on these lines:

For line: 2 x + y = 6, we calculate coordinates of various points:

at X = 0, 2 (0) + y = 6 ∴ y = 6

at X = 1, 2 (1) + y = 6 ∴ y = 4

at X = 2, 2 (2) + y = 6 ∴ y = 2

at X = 3, 2 (3) + y = 6 ∴ y = 0

Hence, we get the following table: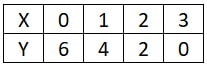

Step 2: Similarly, for line: 2 x – y – 2 = 0, we calculate coordinates of various points:

For line: 2 x – y – 2 = 0, we calculate coordinates of various points:

at X = 0,  2 (0) – y – 2 = 0 ∴ y = – 2

at X = 1,  2 (1) – y – 2 = 0 ∴ y = 0

at X = 2,  2 (2) – y – 2 = 0 ∴ y = 2

at X = 3,  2 (3) – y – 2 = 0 ∴ y = 4

Hence, we get the following table: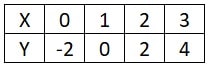

Step 3: Now let’s plot both of these lines connecting each of the points:

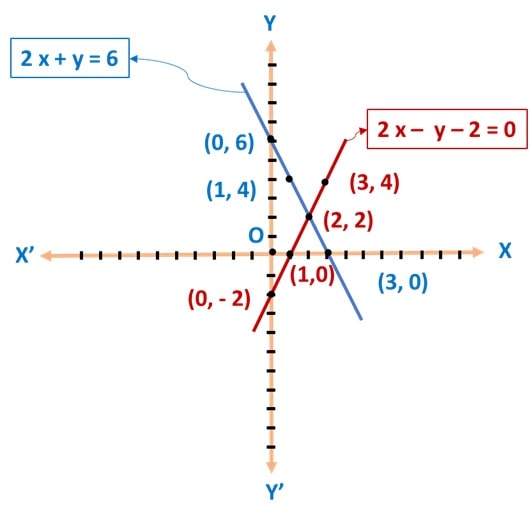
From the diagram, we can see that the lines intersect each other at point (2, 2)

Therefore, the solution of the lines is (2, 2).

Part 2: Area of the triangle formed by two lines and X axis:

Step 4: Line 2 x + y = 6 cuts X – axis at (3, 0)

Line 2 x – y – 2 = 0 cuts X- axis at (1, 0)

Both lines cuts each other at (2, 2)

Hence, the 3 points of the triangle are: A (3,0), B (1, 0) and C (2,2)

AB = √ [(3 – 1)² + (0 – 0)² ] = √4 = 2 units

AC = √ [(3 – 2)² + (0 – 2)² ] = √5 units

BC = √ [(1 – 2)² + (0 – 2)² ] = √5 units

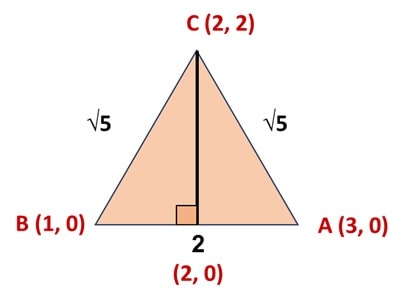
From the triangle, Height = √ (√5)² – 1²) = √(5 – 1) = √4 = 2 units

∴ Area of the triangle = 1/2 x Base x Height

= 1/2 x 2 x 2 = 2 sq units

Therefore, the area of the triangle between lines & X-axis is 2 sq. units.

Please press the “Heart”, if you liked the solution.