Q) A brooch is crafted from silver wire in the shape of a circle with a diameter of 35 cm. The wire is also used to create 5 diameters, dividing the circle into 10 equal sectors as shown in figure. Based on the above information, answer the following questions:
(i) What is the radius of circle? 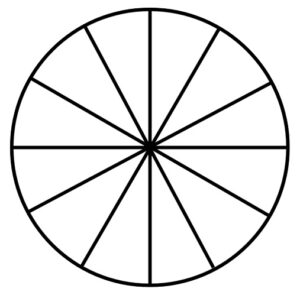
(ii) What is the circumference of the brooch?
(iii) (a) What is the total length of silver wire required?
(iii) (b) What is the area of each sector of the brooch?
(Q 36 – 30/1/3 – CBSE 2026 Question Paper)
Ans:
(i) Radius of the circle:
∵ Diameter of brooch circle = 35 cm (given)
∴ Radius of circle = ![]() = 17.5 cm
= 17.5 cm
Therefore, the radius of the circle is 17.5 cm.
(ii) Circumference of the brooch: 
Circumference = 2 π r
= 2 ![]()
= 110 cm
Therefore, Circumference of the brooch is 110 cm.
(iii) (a) Length of wire required:
Length of wire used in brooch = Circumference of Circle + 5 diameters
Here,
Circumference = 2 π r = 110 cm [calculated in part (ii)]
Length of 5 diameters = 5 x 35 = 175 cm
∴ Total length of wire used = 110 + 175 = 285 cm
Therefore, required silver wire length is 285 cm.
(iii) (b) Area of each sector of the brooch:
Step 1: ∵ Area of a circle = π r 2 
= ![]()
= ![]() cm2
cm2
Step 2: Given that the brooch circle is divided into 10 equal sectors
∴ Area of a sector = ![]()
= ![]() =
= ![]() = 96.25 cm2
= 96.25 cm2
Therefore the area of a sector is 96.25 cm2
Please press the “Heart” button if you like the solution.
