A solid wooden toy is in the shape of a right circular cone mounted

Leave a Comment / surface areas and volumes / By Sapling Academy

Q) A solid wooden toy is in the shape of a right circular cone mounted on a hemisphere of same radius. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the wooden toy. Also, find the total surface area of the toy.

Ans: Let’s draw a diagram for the given question:

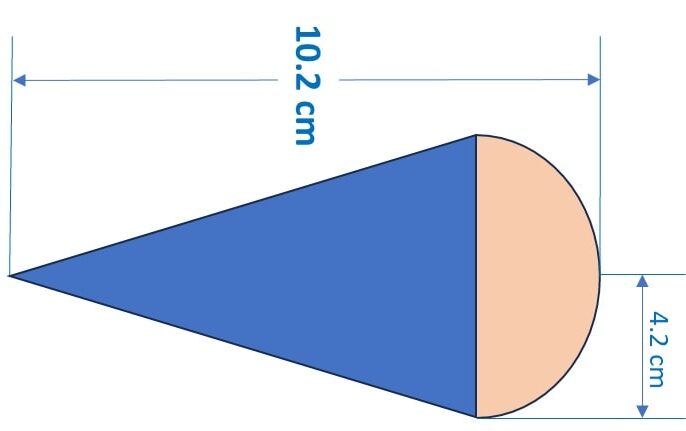
A. Volume of the toy:

Step 1: We are given that, radius of hemishpere = 4.2 cm

Since radius of cone = radius of hemishpere (same base),

Step 2: Height of the sphere = radius of the hemisphere = 4.2 cm

Given the height of the toy, H = 10.2 cm

Height of the cone, H_c= Total height of the cone – height of hemisphere

= 10.2 – 4.2 = 6 cm

Step 3: Volume of the toy = Volume of cone + volume of hemishpere

= $\frac{1}{3} \pi R^2 H_c + \frac{2}{3} \pi R^3$

= $\frac{1}{3}\pi R^2 (H_c + 2R)$

By substituting values of π, R, H_c, we get:

Volume of the toy = $\frac{1}{3} (\frac{22}{7}) (4.2)^2(6 + 2 \times 4.2)$

= 22 x 4.2 x 0.2 x 14.4 = 266.112 cm³

Therefore, the volume of the toy is 266.112 cm³

B. Surface area of the toy:

let’s draw a diagram to calculate slant height of the cone: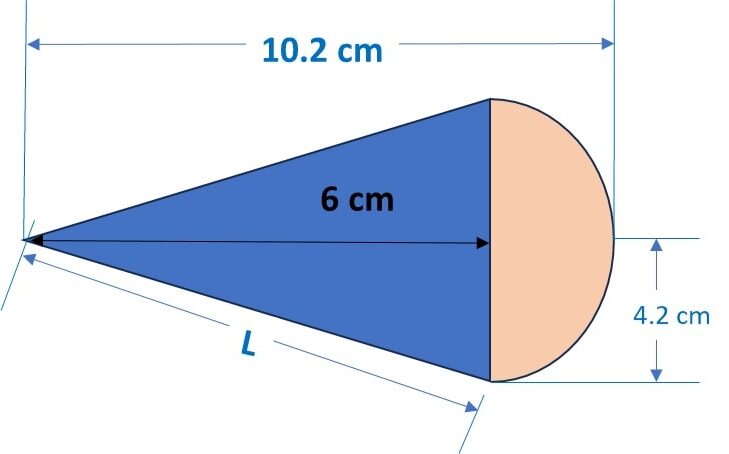

Step 1: Slant height of the cone, L = $\sqrt {(4.2)^2 + (6)^2}$

= 6 √ 1.49 = 7.32 cm

Step 2: Total surface area of the toy = Curved surface area of the cone + surface area of the hemisphere

= π R L + 2 π R² = π R (L + 2 R)

By substituting values of π, R, H_cone, we get:

Total surface area of the toy = $\frac{22}{7} (4.2) (7.32 + 2 \times 4.2)$

= 22 x 0.6 x (7.32 + 8.4)

= 13.2 x 15.72 = 207.504

Therefore, the total surface area of the toy is 207.504 cm²

Please press the “Heart”, if you liked the solution.

Leave a Comment Cancel Reply