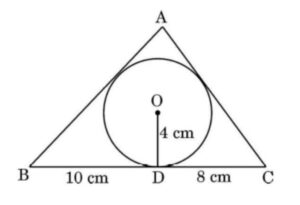
Q)  A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 10 cm and 8 cm respectively. Find the lengths of the sides AB and AC, if it is given that area ▲ ABC = 90 cm².

Ans: Let’s join Point A, B, C with center O and also consider that circle touches AB at point E and AC at point F.

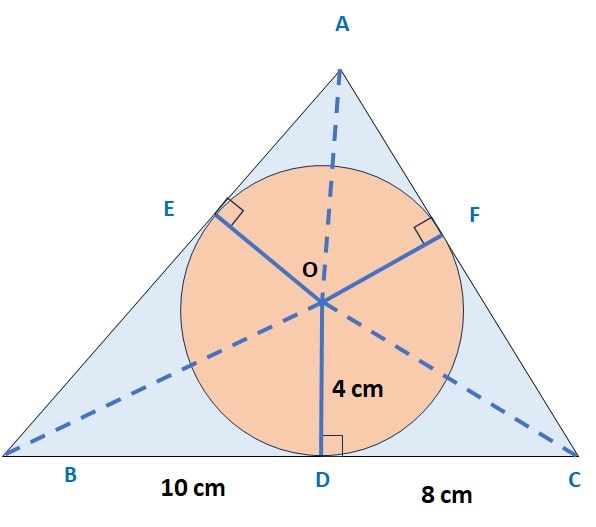
Here, BD = BE = 10 cm (tangents on a circle from same point)

Similarly, CD = CF = 8 cm (given)

and AE = A F  = x (not given)

AB = AE + BE = 10 + x  and AC = AF + CF = 8 + x ……………… (i)

Next, Area of Δ ABC = Area Δ AOB + Area Δ OBC + Area Δ OCA

90 = OE x AB + OD x BC + OF x AC

Since OE = OD = OF = 4 cm                         (radii of circle)

We get, 90 = x 4 (AB + BC + AC)

45 = (10 + x + 18 + 8 + x)                         ……. from equation (i)

2 x = 9 or x = 4.5

Hence, AB = 10 + 4.5 = 14.5 cm and AC = 8 + 4.5 = 12.5 cm

Therefore, AC is 14.5 cm and AC is 12.5 cm