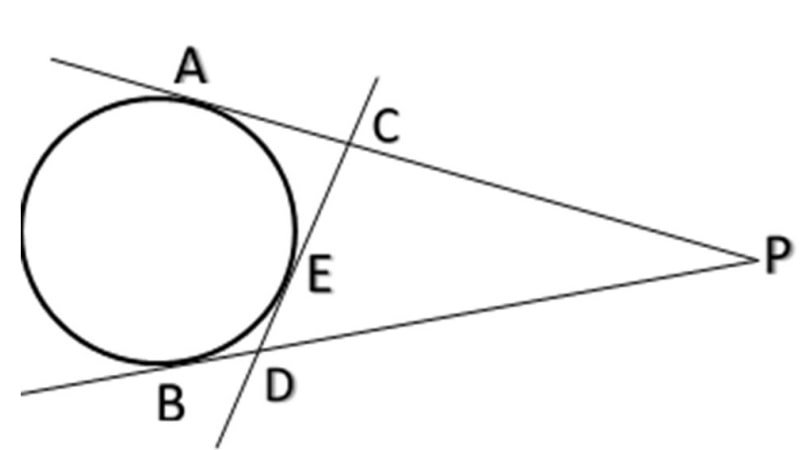
Q) From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At a point E on the circle, a tangent is drawn to intersect PA and PB at C and D, respectively. If PA =  10 cm, find the perimeter of ∆PCD.

Ans:

Let’s draw a diagram and plot the given information.

(Note: your question will become clearer and your answer will never be wrong if you draw a diagram)

We know that the tangents drawn from a point on same circle are equal, therefore:

PA = PB = 10 cm (given)

Perimeter of Δ PCD = PC + CD + PD  ………………………………. (i)

Since E is the point on CD, hence, CD = CE + ED ……………. (ii)

Since BD and ED are the tangents from same point D, therefore BD = ED

Similarly, AC and CE are the tangents from same point C, therefore AC = CE

Substituting both of these values in equation (ii),

we get: CD = AC + BD …………. (iii)

Now substituting this from equation (iii) into equation (i), we get:

Perimeter of Δ PCD

= PC + (AC + BD) + PD

= (PC + AC) + (BD + PD)

= AP + BP = 10 + 10 = 20 cm

Therefore, the perimeter of Δ PCD is 20 cm