ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and

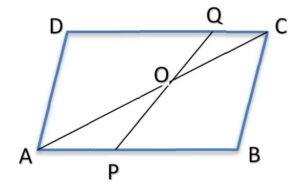
Q) ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

Ans:

Given that ABCD is a parallelogram. Therefore, AB ǁ CD and BC ǁ AD

Since, Point P divides AB in the ratio 2:3

Therefore, if AB = a, then AP = $\frac{2}{5}$ a and BP = $\frac{3}{5}$ a

Since, Point Q divides CD in the ratio 4:1

Therefore, since CD = AB = a, then DQ = $\frac{4}{5}$ a and QC = $\frac{1}{5}$ a

Let’s look at Δ AOP and Δ QOC,

∠ AOP = ∠ QOC (vertically opposite angles)

∠ OAP = ∠ QCO (interior angles)

Therefore, Δ AOP $\sim$ Δ QOC

Hence, $\frac{OA}{OC}$ = $\frac{AP}{QC}$

$\Therefore$ , $\frac{OA}{OC}$ = $\frac{\frac{2}{5}a}{\frac{1}{5}a}$

$\frac{OA}{OC}$ = $\frac{2}{1}$

OC = $\frac{1}{2}$ OA

Therefore, it is proved that OC is half of OA.

Contact us