Q) If a hexagon ABCDEF circumscribes a circle, prove that AB + CD + EF = BC + DE + FA.

(Q 31B – 30/2/2 – CBSE 2026 Question Paper)

Ans:  Let’s first draw a diagram for the given question:

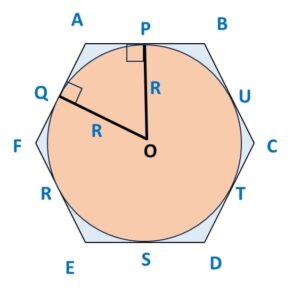
Let ABCDEF be the Heaxagon which is circumscribed on a circle. This circle has Center O and radius R.

Now let P, Q, R, S, T and U be the points on which hexagon touches the circle.

Step 1: Let’s start with point A. AP and AQ are the two tangents drawn on same circle, ∴ AP = AQ

Similarly, From point B, BP and BU are the two tangents drawn on same circle, ∴ BP = BU

Similarly, CU = CT

DT = DS

ES = ER

and FR = FQ

Step 2: Now, AB + CD + EF = (AP + BP) + (CT + DT) +  (ER + FR)

= (AQ + BU) + (CU + DS) + (ES + FQ)   (by substituting values from step 1 identified above)

= (BU + CU) +  (DS + ES) + (FQ + AQ)

= BC + DE + FA

Hence Proved !

Please do press “Heart” button if you liked the solution.