Q)  In the given figure, ∠ CEF = ∠ CFE. F is the midpoint of DC. Prove that .

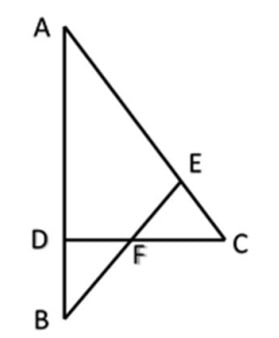
Ans:

Step 1: From given conditions:

1.  ∵  ∠ CEF = ∠ CFE

∴ CE = CF (sides of opp. Angles)

2. ∵  F is midpoint of CD

∴ FD = CF

∴ CE = CF = FD ……… (i)

Step 2: Construct to find relation:

Let’s draw DG ǁ BE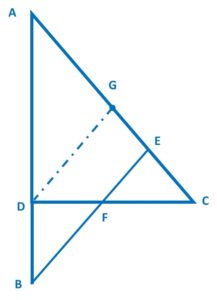

∴ by Basic Proportionality Theorem in Δ ABE:    ………… (ii)

Step 3: establish co-relation:

∴ by Mid Point Theorem in Δ GDC : 

∵  DF = FC ……. from equation (i)

∴ =  1 = 

∴ GE = CE

∵  CE = CF = FD ….. from equation (i)

∴ CE = CF = FD = GE  ……. (iv)

Step 4: Proving the relation:

∵     ……. from equation (ii)

and GE = FD ………… from equation (iv)

∴   

Hence Proved!