Q) In the given figure, AC is the diameter of the circle with centre O.

CD is parallel to BE.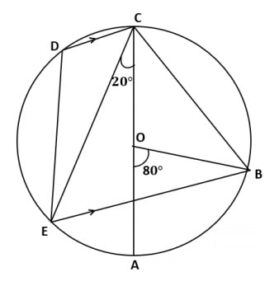 

∠AOB = 80⁰ and ∠ACE = 20⁰.

Calculate:

(a) ∠ BEC

(b) ∠ BCD

(c) ∠ CED

ICSE Specimen Question Paper (SQP) 2026

Ans:

Step 1: AC is the straight line and hence ∠ AOB + ∠ BOC = 180°

∴ ∠ BOC = 180° – ∠ AOB

∠ AOB = 80° (given)

∴ ∠ BOC = 180° – 80° = 100°

Step 2: Let’s look at chord BC in the given figure:

Chord BC is making ∠ BOC at the centre and ∠ BEC at the circumference.

By angle at the centre theorem, we know that the angle subtended by a chord at the centre is twice the angle subtended on the circumference.

∴ ∠ BOC = 2 ∠ BEC

∴ ∠ BEC = ∠ BOC / 2

∴ ∠ BEC = 100° / 2 = 50°.      (∠BOC = 100° calculated above)

Therefore, the value of ∠ BEC is 50°.

(b) Value of ∠BCD:

Step 3: Let’s connect chord AB and check the following: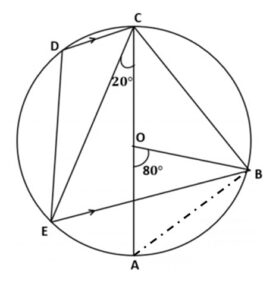 

Chord AB is making ∠AOB at the centre and ∠ACB at the circumference.

By angle at the centre theorem, we know that the angle subtended by a chord at the centre is twice the angle subtended on the circumference.

∴ ∠AOB = 2 ∠ACB

∴ ∠ACB = ∠AOB / 2

∴ ∠ACB = 80°/ 2 = 40°.       (∠AOB = 80° given in the figure)

Step 4: Next, we are given that CD is parallel to BE and when CE cuts these lines, alternate angles will be equal

hence, ∠ECD = ∠BEC

We just proved above that ∠BEC = 50°         

∴ ∠ECD = 50°

Step 5: Now, from the given figure,

∠BCD = ∠BCA + ∠ACE + ∠ECD

∴ ∠BCD = 40° + 20° + 50° = 110°    (∠ACE = 20° given in the figure)

Therefore, the value of ∠BCD is 110°

(c) Value of ∠ CED:

Step 6: From the diagram, we can see that BCDE is a cyclic quadrilateral, whose all 4 vertices are lying on the circle’s circumference.

We know that the sum of opposite angles of a cyclic quadrilateral is 180°.

∴ ∠BCD + ∠BED = 180°

∴ ∠BED = 180° – ∠BCD 

∴ ∠BED = 180° – 110°             (∠BCD = 110° calculated above)

∴ ∠BED = 70°.

Step 7: From the given figure, we can see that

∠BED = ∠BEC + ∠CED

∴ ∠CED = ∠BED – ∠BEC

 ∴ ∠CED = 70° – 50° = 20°.          (∠BEC = 50° calculated above)

Therefore, the value of ∠CED is 20°.

Please do press “Heart” button if you liked the solution.