Q) In the given figure (not drawn to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
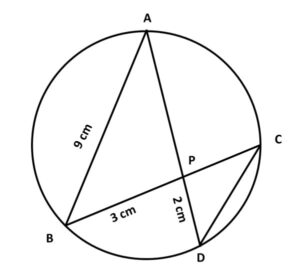
(a) Prove that ∆APB ~ ∆CPD.
(b) Find the length of CD.
(c) Find area ∆APB : area ∆CPD.
ICSE Specimen Question Paper (SQP)2026
Ans:
a) Prove Δ AΡΒ ~ Δ CPD:
Let’s compare Δ APB and Δ CPD :
Here, ∠BAP = ∠ BCD (angles subtended by same segment)
similarly, ∠ ABP = ∠ CDP (angles subtended by same segment)
∴ by AA similarity rule,
Δ APB ~ Δ CPD .…….. Hence Proved !
b) Length of CD:
Let’s look at Δ APB and Δ CPD:
We just proved that these are similar triangles,
∴ ![]() … (i)
… (i)
By substituting the given values, we get:
![]()
∴ CD = ![]()
∴ CD = 6 cm
Therefore, length of CD is 6 cm.
(c) Area ∆APB : Area ∆CPD:
Since Area of a triangle is given by 1/2 x Height x Base
∴ Area ∆APB = ![]() x AP x BP
x AP x BP
Similarly, Area ∆CPD = ![]() x CP x PD
x CP x PD
∴ Area ∆APB : Area ∆CPD = 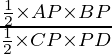
= ![]()
= ![]()
From equation (i), we have ![]()
∴ Area ∆APB : Area ∆CPD = ![]() =
= ![]()
By substituting the given values, we get:
Area ∆APB : Area ∆CPD = ![]() =
= ![]()
Therefore, Area ∆APB : Area ∆CPD = 9:4
Please press the “Heart” button, if you like the solution.
