Q) Pookalam is the flower bed or flower pattern designed during Onam in Kerala. It is similar as Rangoli in North India and Kolam in Tamil Nadu.

During the festival of Onam , your school is planning to conduct a Pookalam competition. Your friend who is a partner in competition, suggests two designs given below. Observe these carefully.

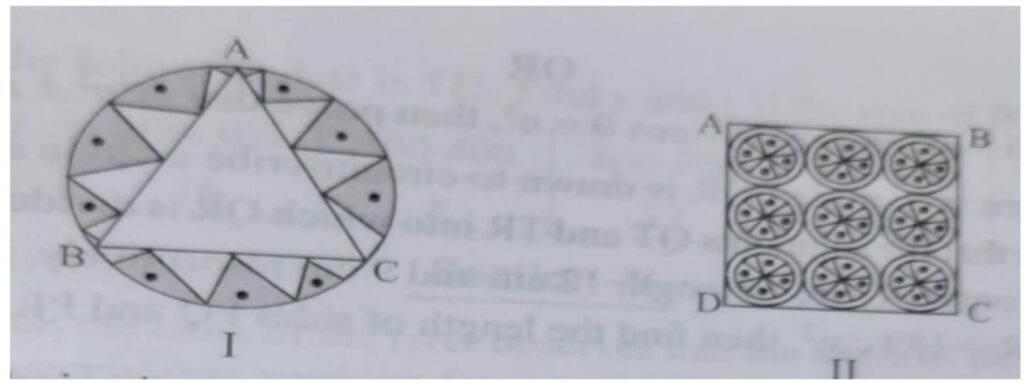
Design I: This design is made with a circle of radius 32cm leaving equilateral triangle ABC in the middle as shown in the given figure.
Design II: This Pookalam is made with 9 circular design each of radius 7cm.

Refer Design I:
1. The side of equilateral triangle is
a) 12√3 cm         b) 32√3 cm             c) 48cm               d) 64cm

2. The altitude of the equilateral triangle is
a) 8 cm               b) 12 cm                 c) 48cm               d) 52cm

Refer Design II:
3. The area of square is:
a) 1264 cm2        b) 1764 cm2          c) 1830 cm2        d) 1944 cm2

4. Area of each circular design is:
a) 124 cm2          b) 132 cm2            c) 144 cm2          d) 154 cm2

5. Area of the remaining portion of the square ABCD is
a) 378 cm2          b) 260 cm2            c) 340 cm2          d) 278 cm2

Ans:  Let’s start from Design 1:

1. Side of Equilateral Triangle, BC:

It is given that the radius of the circle is 32 cm and Δ ABC is a equilateral triangle 

Let’s consider O is the center of the circle and connect O with vertices A, B and C.

Here OA = OB = OC = 32 cm (being radius of the circle)

Here Since Δ ABC is a equilateral triangle,

∴ all angles will be 60⁰

∠ A = 60⁰

Next, since the angle subtended by an arc at the centre of a circle is double of the angle subtended by same arc at any point on the remaining part of the circle.

∴ ∠ BOC = 2 x ∠ BAC  = 2 x 60 = 120⁰

Next, let’s take Δ ABC and draw line OD perpendicular to BC.

Since Δ BOD and Δ COD are similar triangles,

∴ ∠ BOD = ∠ BOD = = 60⁰

Next, we will look in Δ BOD: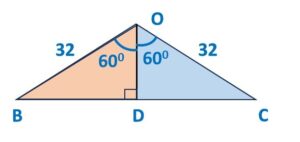

∵ Sin (∠ BOD) =

∴ Sin 60⁰ =

∴

∴ BD = =  16√3

Next, in Δ ABC, BD = BC

∴ BC = BD + DC = 2 x BD

∴ BC = 2 x 16√3 = 32√3

Hence, the side of equilateral triangle is: 32√3 cm

Therefore, Option (b) is correct.

2. Altitude of Equilateral triangle (AD):

Let’s relook in Δ BOD:

∵ cos (∠ BOD) =

∴ cos 60⁰ =

∴

∴ OD = =  16

Next, in Δ ABC, we can see that the altitude AD = AO + OD

We already have OA, the radius of the circle = 32 cm

OD, we calculated as 16 cm

∴ AD = AO + OD = 32 + 16 = 48 cm

Hence, the altitude of equilateral triangle is 48 cm

Therefore, Option (c) is correct.

Now in Design II:

3. Area of Square:

Let’s start with the figure:

We are given that each circle is of 7 cm radius,

∴ the diameter of each circle is 14 cm

Since each side comprises of 3 circles,

∴ length of side = 3 x diameter of a circle = 3 x 14 = 42 cm

Thus we get a square of 42 cm side.

Now, Area of a square is given by (side)²

∴ Area = (42)²  = 1764 cm²

Hence, the area of the square is 1764 cm²

Therefore, Option (b) is correct.

4. Area of each circular design:

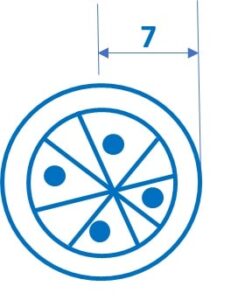It is given that the circular design has radius of 7 cm

∵ Circle’s area is given by = π r²

∴ Area of the given circlular design = π (7) ²

= (7)²

= 154 cm²

Hence, area o f each circular design is 154 cm²

Therefore, Option (d) is correct.

5. Area of shaded region:

Looking at the diagram, we can clearly see that the square comprises of 9 circular designs.

There is area which is uncovered by these circullar designs and we need to calculate area of these uncovered region.

Since Area of Square = 1764 cm²  (from part 3)

Area of one circular design = 154 cm² (from part 4)

∴ Area covered by 9 circular designs = 9 x 154 = 1386 cm²

∵ The area of shaded region = Area of square – area of 9 circular designs

 = 1764 – 1386 = 378 cm²

Hence, the area of shaded region is 378 cm².

Therefore, Option (a) is correct.

इति समाधानम्

Please do press “Heart” button if you liked the solution.