Q) Scale drawing of an object is the same shape at the object but a different size. The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The scale is written as a ratio. The ratio of two corresponding sides in similar figures is called the scale factor

Scale factor= length in image / corresponding length in object

If one shape can become another using revising, then the shapes are similar. Hence, two shapes are similar when one can become the other after a resize, flip, slide or turn. In the photograph below showing the side view of a train engine. Scale factor is 1:200

This means that a length of 1 cm on the photograph above corresponds to a length of 200cm or 2 m, of the actual engine. The scale can also be written as the ratio of two lengths.

1. If the length of the model is 11cm, then the overall length of the engine in the photograph above, including the couplings(mechanism used to connect) is:

a) 22cm                 b) 220cm                     c) 220m                   d) 22m

2. What will affect the similarity of any two polygons?
a) They are flipped horizontally
b) They are dilated by a scale factor
c) They are translated down
d) They are not the mirror image of one another.

3. What is the actual width of the door if the width of the door in photograph is 0.35cm?
a) 0.7m                  b) 0.7cm                      c) 0.07cm                d) 0.07m

4. If two similar triangles have a scale factor 5 : 3 which statement regarding the two triangles is true?
a) The ratio of their perimeters is 15 : 1
b) Their altitudes have a ratio 25 : 15
c) Their medians have a ratio 10 : 4
d) Their angle bisectors have a ratio 11 : 5

5. The length of AB in the given figure:

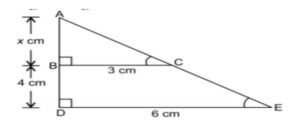
a) 8cm                  b) 6cm                          c) 4cm                      d) 10cm

Ans:

1) Length of the engine:

Since it is given that the Scale factor is 1 : 200

Therefore, = Scale Factor

∴

∴ Overall length of engine = 11 x 200 cm

= 2200 cm or 22m

Therefore, Option d) is correct.

2. Similarity of Polygons:

Let’s consider hexagon as our specimen polygon and check each option one by one:

(a) Flipping horizontally:

As we can see, after flipping the size of the new polygon is same as original one

Since they are similar

Hence similarity of both polygons is not affected

(b) Dilating by a scale factor: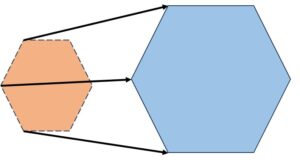   

When a polygon is dilated by a scale factor it means its each side is being dilated in same ratio.

As we can see in the image, after dilating, both polygons remain similar

Hence similarity of both polygons is not affected

(c) Translating down:   

Lets look at the side image:

If you look closely, each side of the new polygon is just same as earlier one

Hence, even after translating down, the size of the new polygon is same as original one

Since they are similar

Hence similarity of both polygons is not affected

(d) Not a mirror image: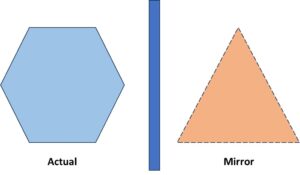 

Let’s look at side image:

We took hexagon and in the mirror image it shows a triangle

since the shape and size of new polygon gets changed, they are no longer similar.

Hence their similarity of polygons definitely gets affected

Therefore, Option d) is correct.

3. Actual width of the door:

Since it is given that the Scale factor is 1 : 200

Therefore, = Scale Factor

∴

∴ Actual width of door = 0.35 x 200

= 70 cm or 0.7 m

Therefore, Option a) is correct.

4. Validity of statements:

Let’s draw two triangles and examine each statement one by one: 

a) Perimeters:

Since the sides of the similar triangles are in ratio of 5:3

∴ Perimeter’s ratio =

=

∴ Perimeters of the triangles are in ratio of 5:3

Hence, the statement “ratio of their perimeters is 15 : 1” is not true

(b) Altitudes:       

Since the triangles are in the ratio of 5:3

Therefore each of the sides are in the ratio of 5:3, including altitudes.

Now, in the statement, it is given that the altitudes are in ratio of 25:15

∴

Hence, the statement “altitudes have a ratio 25 : 15” is true

(Note: Though this becomes the answer if it is a single choice question and we can end the solving of this part here. But let’s check other options as well – this will be helpful if the question comes in multiple choice question.)

(c) Medians:    

Let’s look at the line AD and PS in the side image.

If we consider D and S are mid points, then lines AD and PS are medians.

Since it is given that the triangles are in the ratio of 5:3

Therefore each of the sides are in the ratio of 5:3,

∴ Medians ratio:

Hence, the statement “medians have a ratio 10 : 4” is not true

(d) Angle Bisectors:

Let’s look at the line AD and PS in the side image.

If we consider AD bisects ∠ A  and PS bisects ∠ P, then lines AD and PS are angle bisectors.

Since it is given that the triangles are in the ratio of 5:3

Therefore each of the sides are in the ratio of 5:3,

∴ Angle bisectors ratio:

Hence, the statement “angle bisectors have a ratio 11 : 5” is not true

Hence, we can say that only one statement “altitudes have a ratio 25 : 15” is true

Therefore, Option b) is correct.

5. Length of AB:

Let’s look at the diagram:

We can see that the Δ ABC and Δ ADE are similar

∴ ratio of 2 sides of Δ ABC will be equal to ratio of 2 sides of Δ ADE

∴

From the diagram, we have BC = 3 cm, DE = 6 cm and BD = 4 cm

if we consider AB = X cm then AD = AB + BD = X + 4 cm

By transferring values in  the above equation, we get:

∴

∴ 6 X = 3 (X + 4)

∴ 2X = X + 4

∴ 2 X – X = 4

∴ X = 4

Therefore, length of AB is 4 cm

इति समाधानम्

Please do press “Heart” button if you liked the solution.