Q) Rohan wants to measure the distance of a pond during the visit to his native. He marks points A and B on the opposite edges of a pond as shown in the figure below. To find the distance between the points, he makes a right-angled triangle using rope connecting B with another point C are a distance of 12m, connecting C to point D at a distance of 40m from point C and the connecting D to the point A which is are a distance of 30m from D such the <ADC=90°

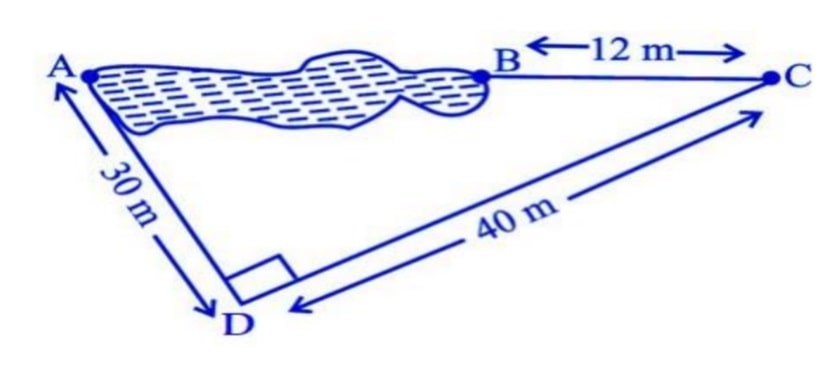
1. Which property of geometry will be used to find the distance AC?
a) Similarity of triangles                       b) Thales Theorem
c) Pythagoras Theorem                            d) Area of similar triangles

2. What is the distance AC?
a) 50m                   b) 12m                         c) 100m                   d) 70m

3. Which is the following does not form a Pythagoras triplet?
a) (7,24,25)           b) (15,8,17)                  c) (5,12,13)              d) (21,20,28)

4. Find the length AB?
a) 12m                   b) 38m                         c) 50m                     d) 100m

5. Find the length of the rope used.
a) 120m                b) 70m                          c) 82m                      d) 22m

Ans: Let’s take each part one by one:

1) Property of Geometry:

Looking at the diagram given: 

We can see that figure ADC is forming a triangle with its sides AD, DC and AC.

Its ∠ ADC is 90⁰ (given)

Therefore, Δ ADC is a right angled triangle.

Here, we are given length of sides AD and DC, and we can use Pythagorus Theorem to calculate length of AC

Therefore, Option c) is correct.

2. Distance AC:

Now in Δ ADC, we have values as under:   

Side AD = 30 m, Side DC = 40 m

∴ By applying Pythagorus theorem, we can write that: AC² = AD² + DC²

By putting values of AD and DC, we get:

AC² = (30)² + (40)² = 900 + 1600 = 2500 = (50)²

∴ AC = 50 m

Therefore, Option a) is correct.

3. Non-Pythagorean triplet:

A Pythagorean triplet is a set of 3 numbers where square of the largest number is equal to sum of squares of other two numbers.

Hence, if A, B and C are a set of 3 numbers and C is the largest of the three numbers,

Here, if C²  = A² + B², then (A, B, C) will be called Pythagorean triplet

Let’s check each of the options one by one:

a) (7, 24, 25):

Here, 25 is the largest number

∴ (7)² + (24)²  = 49 + 576  = 625 = (25)²

Hence, (7, 24, 25) is a Pythagorean Triplet.

b) (15, 8, 17):

Here, 17 is the largest number

∴ (15)² + (8)²  = 225 + 64 = 289 = (17)²

Hence, (15, 8, 17) is a Pythagorean Triplet.

c) (5, 12,13):

Here, 13 is the largest number

∴ (5)² + (12)² = 25 + 144 = 169 = (13)²

Hence, (5, 12, 13) is a Pythagorean Triplet.

d) (21, 20, 28):

Here, 28 is the largest number

∴ (21)² + (20)² = 441 + 400  = 841  ≠ (28)²

Hence, (21, 20, 28) is not a Pythagorean Triplet.

Therefore, Option d) is correct.

4. Length of AB:

Let’s look at the diagram again:   

We are given BC = 12 m

We just calculated AC = 50 m (using Pythagorean theorem in part 2)

∵ AC = AB + BC

∴ AB = AC – BC  =  50 – 12 = 38m

Therefore, Option b) is correct.

5. Length of Rope:

Here, if we look at the diagram again, we can see that the rope length is sum of the sides of triangle except the pond.

∴ Rope length = AD + DC + BC

= 30 + 40 + 12 = 82 m

Therefore, Option c) is correct

इति समाधानम्

Please do press “Heart” button if you liked the solution.