Q) Prove that: ![]()
Ans: Let’s start from LHS
![]()
= 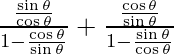
= ![]()
= ![]()
= ![]()
We know that, a3−b3 formula is = (a−b)(a2 + b2 + ab)
![]()
= ![]()
= ![]()
= ![]()
= sec θ cosec θ + 1
= 1 + sec θ cosec θ = RHS
Hence Proved
Q) Prove that: ![]()
Ans: Let’s start from LHS
![]()
= 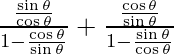
= ![]()
= ![]()
= ![]()
We know that, a3−b3 formula is = (a−b)(a2 + b2 + ab)
![]()
= ![]()
= ![]()
= ![]()
= sec θ cosec θ + 1
= 1 + sec θ cosec θ = RHS
Hence Proved