Q) The inner and outer radii of a hollow cylinder surmounted on a hollow hemisphere of same radii are 3 cm and 4 cm respectively. If height of the cylinder is 14 cm, then find its total surface area (inner and outer).

Ans: 

VIDEO SOLUTION

STEP BY STEP SOLUTION

Let’s draw a diagram to better understand the question:

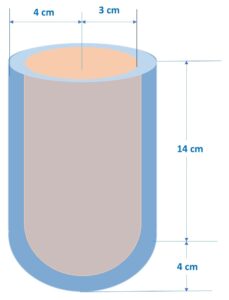
Here, in this question, it is given that:

Outer radii (of sphere and cylinder), R₁ = 4 cm

Inner radii (of sphere and cylinder), R₂ = 3 cm

Height of cylinder, H = 14 cm

Total surface area = Outer Surface Area of Cylinder + Outer Surface Area of Hemisphere + Surface Area of Circular Ring at the top + Inner Surface Area of Cylinder + Inner Surface Area of Hemisphere

= 2 π  R₁ H  + 2 π R₁ ²  + π [ R₁ ² – R₂ ² ] + 2 π R₂ H + 2 π R₂ ² 

= 2 π  x 4 x 14 + 2 π (4) ²  + π [ (4) ² – (3) ² ] + 2 π x 3 x 14 + 2 π (3) ² 

= 112 π  + 32 π  + 7 π + 84 π  + 18 π = 253 π

= 253 x = = 795.14 cm²

Therefore, the total surface area (inner and outer) of the shape is 795.14 cm²

Please press the “Heart”, if you like the solution.