Leave a Comment / surface areas and volumes / By

Q) The slant height of a frustum of a cone is 4 cm and the perimeters of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Ans:

STEP BY STEP SOLUTION

Let’s draw a diagram for this question to understand it better:  

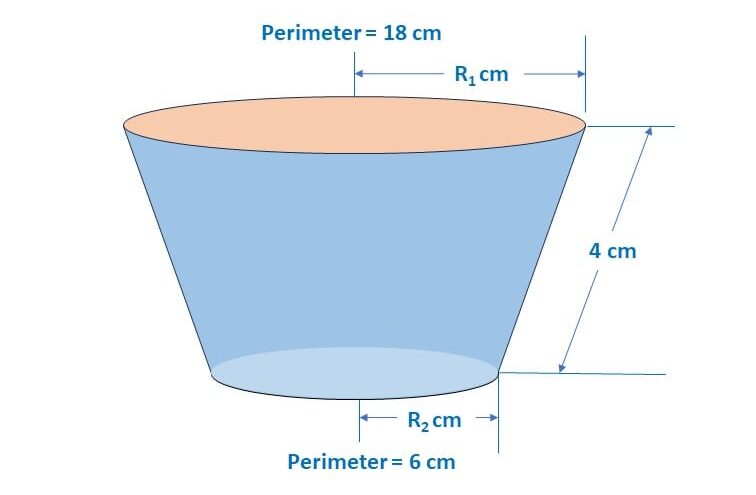
The slant height of a frustum of a cone is 4 cm and the perimeters of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.

[Note: Since a frustum is a combination of 2 cones; hence its curved surface area is difference of curved surface area of 2 cones.]

Step 1:

The Perimeter of a circle, P = 2 π R, 

Hence, radius of a circle, R = \frac{P}{2\pi}

Here, we have perimeter of upper circular end, P1 = 18 cm

∴ the radius of upper end, R1 = \frac{18}{2\pi} = \frac{9}{\pi}

Similarly, perimeter of lower circular end, P2= 6 cm

∴ the radius of lower end, R2 = \frac{6}{2\pi} = \frac{3}{\pi}

Step 2:

Now, the curved surface area of a Frustum is given by: π x L x (R1 + R2)

Here, we have L = 4 cm, R1= \frac{3}{\pi} cm, R2 = \frac{9}{\pi} cm,

∴ the curved surface area of given Frustum = \pi (4) (\frac{9}{\pi} + \frac{3}{\pi})

= \pi \times 4 \times \frac{12}{\pi} = 48 cm2

Therefore, the curved surface area of the frustum is 48 cm2

 

Please do press “Heart” button if you liked the solution.

Related Posts

Leave a Comment

Your email address will not be published. Required fields are marked *

Scroll to Top