Q) Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in LL and AD (produced) in E. Prove that EL = 2BL.

Ans: 

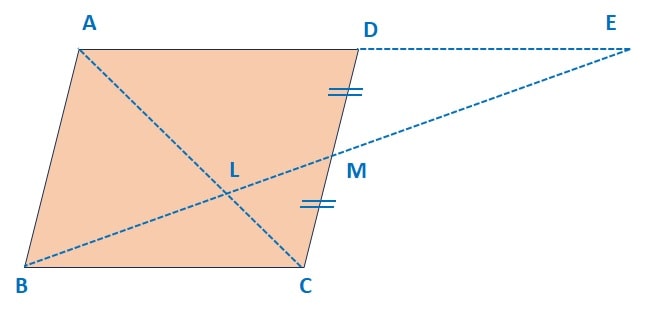
In Δ BMC and Δ EMD,

MC = MD (given)

∠ CMB = ∠ EMD              (Opposite angles)

∠ MBC = ∠ MED              (Interior angles)

Δ BMC ~ Δ EMD

Hence, BC = DE

But, BC = AD  (by ABCD is a parallelogram)

AE = 2 BC……………. (i)

∠ CAE = ∠ LCB                  (Interior angles)

∠ LBC = ∠ LEA                  (Interior angles)

Δ LBC ~ Δ LAE

Hence,

or,

Hence, = 2

Therefore, EL =  2 BL    ………… Hence proved