Q) Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles. The height of Vijay’s house if 20m when Vijay’s house casts a shadow 10m long on the ground. At the same time, the tower casts a shadow 50m long on the ground and the house of Ajay casts 20m shadow on the ground.
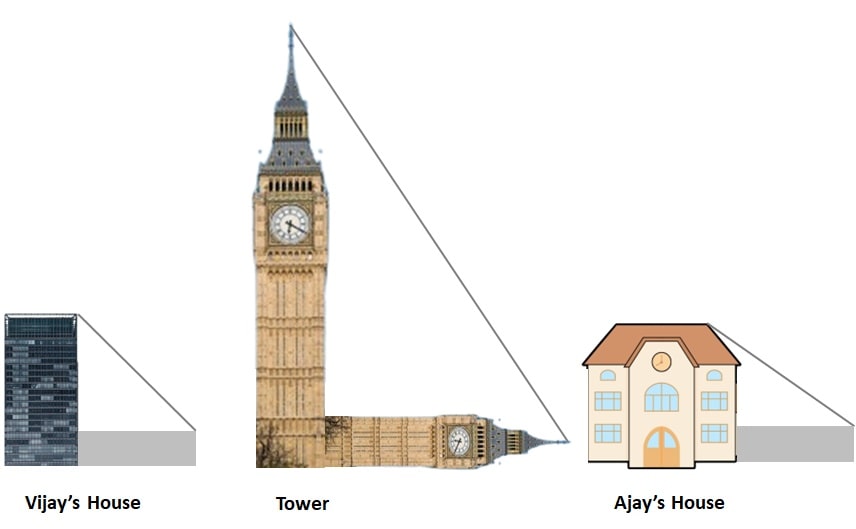
1. What is the height of the tower?
a) 20m b) 50m c) 100m d) 200m
2. What will be the length of the shadow of the tower when Vijay’s house casts a shadow of 12m?
a) 75m b) 50m c) 45m d) 60m
3. What is the height of Ajay’s house?
a) 30m b) 40m c) 50m d) 20m
4. When the tower casts a shadow of 40m, same time what will be the length of the shadow of Ajay’s house?
a) 16m b) 32m c) 20m d) 8m
5. When the tower casts a shadow of 40m, same time what will be the length of the shadow of Vijay’s house?
a) 15m b) 32m c) 16m d) 8m
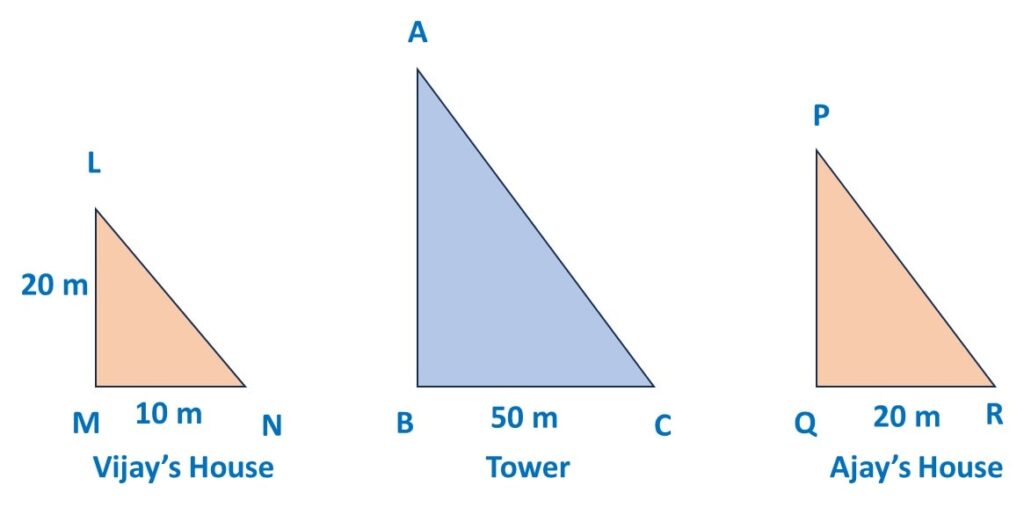
Ans: We are given following information:
Height of Vijay’s house = 20m
Shadow length of Vijay’s house = 10m
Shadow length of Tower = 50m
Shadow length of Ajay’s house = 20m
Let’s draw a simple diagram with above information and find out answers:
1. Height of the tower:
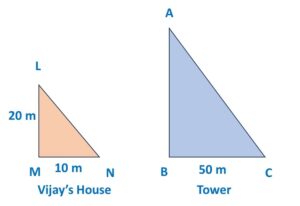
Now to calculate the tower’s height, we need to focus on Vijay’s house and Tower only,
hence we will look at this image:
Here, we need to find out the height of the tower AB.
By Similar triangles property:
![]()
From given data, we get:
![]()
∴ AB = 2 x 50 = 100
∴ Height of the tower is 100 m,
Therefore, Option c) is correct.
2. Length of the shadow of the tower when Vijay’s house shadow is 12m:
Here, we are given different shadow length for Vijay’s house as 12 m
We already have Height of Vijay’s house is given as 20 m 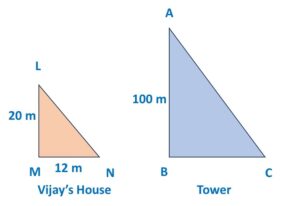
and we just calculated the height of tower as 100m
Hence, let’s draw a revised image with above data:
We need to calculate Shadow of the tower, BC.
Now by Similar triangles property:
![]()
∴ ![]()
∴ BC = ![]() = 60
= 60
∴ Shadow length of tower is 60 m
Therefore, Option d) is correct.
3. Height of Ajay’s house:
Now we will look at Ajay’s House and Vijay’s house only 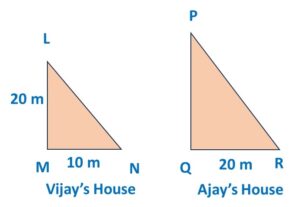
Our focused image will be:
By Similar triangles property:
![]()
From given (original) data, we get:
![]()
∴ PQ = 2 x 20 = 40
∴ Height of Ajay’s House is 40 m
Therefore, Option b) is correct.
4. Shadow length of Ajay’s House if Tower’s shadow length is 40m:
Now we will look at Ajay’s house and Tower and supply new data. 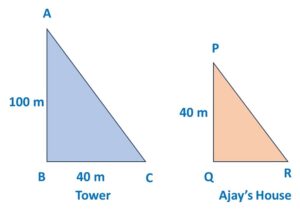
We need to find out Shadow length of Ajay’s house, QR
By Similar triangles property:
![]()
From given data, we get:
![]()
∴ QR = ![]() = 16
= 16
∴ Shadow length of Ajay’s house is 16 m
Therefore, Option a) is correct.
5. Shadow length of Vijay’s House when Tower’s shadow length is 40m:
Now we will look at Vijay’s house and Tower and supply new data. 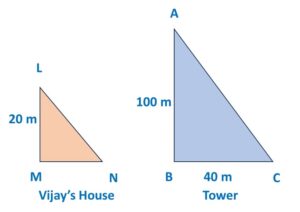
We need to find out Shadow length of Vijay’s House, MN
By Similar triangles property:
![]()
From given data, we get:
![]()
∴ MN = ![]() = 8
= 8
∴ Shadow length of Vijay’s house is 8 m
Therefore, Option d) is correct
इति समाधानम्
Please do press “Heart” button if you liked the solution.
