Q) The angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the distance of the cloud from the point of observation is .

Ans:

Step 1: Let’s draw a diagram for the given question:

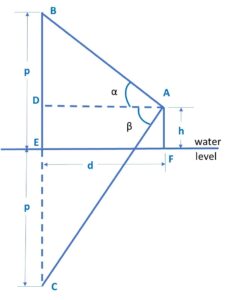
Here, point of observation is A, cloud is at point B and cloud’s reflection is at point C.

Here, let’s consider the height of AF is h and line AD or Line EF is d, height of cloud from water level is p and CE is also p (reflection).

We need to find length of line AB.

Step 2: Let ‘s start with Δ ADB,

tan ∠ DAB = 

∴ tan α =

∴ p – h = d tan α

∴ p = h + d tan α  ……….. (i)

Step 3: Next in Δ ADC,

tan ∠ DAC = 

∴ tan β =

∴ p + h = d tan β

∴ p = d tan β – h ….. (ii)

Step 4: From equations (i) and (ii), we compare values of p:

h + d tan α  = d tan β – h

∴ 2 h = d tan β – d tan α

∴ 2 h = d (tan β – tan α)

∴ d = ……… (iii)

Step 5: Δ ADB, cos ∠ DAB = 

∴ cos α =

∴ AB = d sec α …… (iv)

Step 6: By substituting value of d from equation (iii),  in equation (iv), we get:

AB = d sec α

∴ AB =

∴ AB =

Hence Proved !

Please press “Heart” button if you like the solution.