Q) If the mode of the following distribution is 55, then find the value of x. Hence, find the mean.

Q35 A – Sample Question Paper – Set 1 – Maths Standard – CBSE 2026
Ans:
Approach: Let’s start calculating the mode value for the given data and it will be calculated in terms of x. We will compare it with given value of 55 and find the value of x. Then we can find value of mean.
Step 1: Since the modal class is the class with the highest frequency.
Let’s consider value of x is not higher than 15, hence 15 is the highest frequency for the given data.
Hence, modal class is “45 – 60”.
Now mode of the grouped data is calculated by:
Mode = L + [ (f1 – f0) / (2 f1 – f0 – f2 ) ] x h
Here,
L = lower class limit of modal class = 45
f1 = frequency of modal class = 15
f0 = frequency of class proceeding to modal class = x
f2 = frequency of class succeeding to modal class = 10
h = class size = 60 – 45 = 15
Let’s put values in the formula and solve:
Mode = L + [ (15 – x ) / (2 (15) – x – 10 ) ] (15)
= 45 + [ (15 – x ) / (20 – x) ] (15)
= 45 + 15 (15 – x ) / (20 – x)
Step 2: Given that the mode value is 55
∴ 45 + 15 (15 – x ) / (20 – x) = 55
∴ 15 (15 – x ) / (20 – x) = 10
∴ 3 (15 – x ) / (20 – x) = 2
∴ 45 – 3 x = 40 – 2 x
∴ 45 – 40 = 3 x – 2 x
∴ x = 5
Therefore, the value of x is 5.
ii. Mean value of the given data:
Step 1: After finding x = 5, here is the updated table: 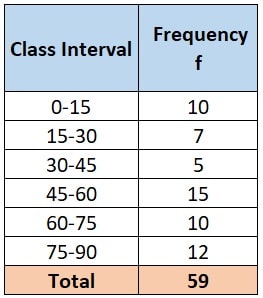
Step 2: Next we calculate midpoints “x” for each group. and then calculate Σf and Σfx.
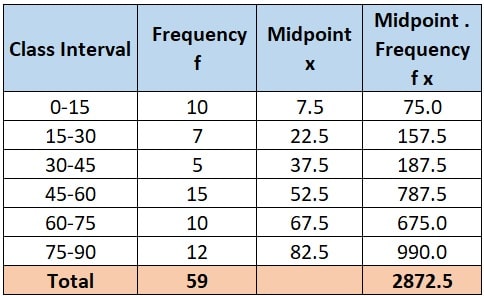
Step 3: We know that, mean of grouped data = Σf x / Σf
= 2872.5 / 59
= 48.69
Therefore, the mean value of data is 48.69
Please do press “Heart” button if you liked the solution
