Using step-deviation method, find mean for the following frequency distribution:

ICSE Specimen Question Paper (SQP) 2026

Ans:

Step 1: From the given frequency distribution table, first we calculate class marks (x) for each class interval.

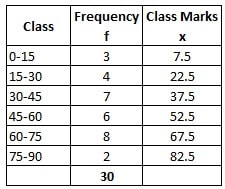
Step 2: we take 45-60 as mean class. Hence, its class marks 52.5 as our assumed mean

∴ A = 52.5

Next, we calculate deviation (d) for each class interval now by deviation, d = x – A

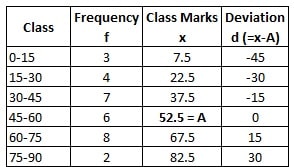
Step 3: We calculate step-deviation (u) for each class interval now:

Step deviation, u =

Here, class width, h is 15 (difference of upper & lower limit of any class width from the given table)

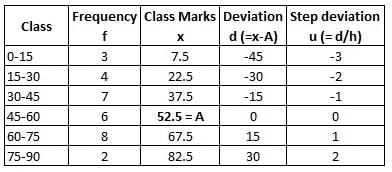
Step 4: Next, we calculate value of (f x u) for each class interval, Also calculate and for given data.

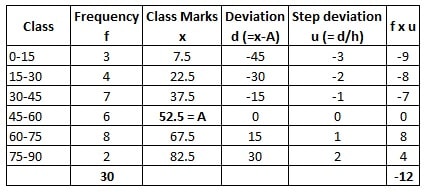
Step 5: Mean = A + x h

from above, we have: A = 52.5,  = – 12,  = 30, h = 15

By substituting the values in the above formula, we get:

Mean = 52.5 + x (15)

= 52.5 – x (15)

= 52.5 – 6 = 46.5

Therefore, the mean value of the given frequency distribution is 46.5.                      

Please press the “Heart” button if you like the solution.