Q) From an external point P, two tangents PA and PB are drawn to the circle with centre O. If ∠PAB=50°, then find ∠AOB

Ans:

Step 1: Let’s draw a diagram with a circle with O as centre.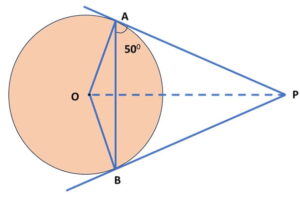 

Let the two tangents PA and PB are drawn from point A on to this circle and touching at points A and B respectively.

AB is the chord and point P is connected with centre O.

Step 2: We know that tangent at a point on a circle is perpendicular to the radius at that point.

∴ ∠ PAO 90⁰

Step 3: ∠ OAB = ∠ PAO – ∠ PAB   

∵ ∠ PAB = 50⁰          (given)

∴ ∠ OAB = 90⁰ – 50⁰ = 40⁰

Step 3: In △OAB,

​∵ OB=OA                (Radii of same circle)

∴ ∠OAB = ∠OBA = 40º

Step 4: Now in △OAB, by angle sum property:

∠ AOB +∠ OAB + ∠ OBA = 180º

∴ $\angle AOB\; +\; 40º\; +40º\; =\; 180º$

∴ $\angle AOB\; +\; 80º\; =\; 180º$

∴ $\angle AOB\; =\; 180º\; –\; 80º$

∴ $\angle \mathrm{AOB}$$=\; 100º$

Therefore, the value of $\angle AOB\; is100º$

Please press the “Heart” button, if you like the solution.