Q) From an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of chord AB. 

Ans:

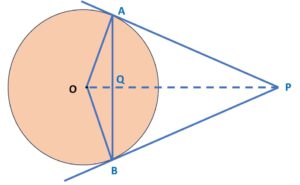
Step 1: Let’s draw a diagram with a circle with O as centre. Let the two tangents PA and PB are drawn from point A on to this circle and touching at points A and B respectively. AB is the chord and point P is connected with centre O.

We need to prove that OP is the perpendicular bisector of chord AB.

To prove the above, we need to prove that:

a) AQ = BQ (for bisecting)

b) ∠ AQP = ∠ BQP = 90⁰ (for OP being on AB)

Step 2: Let’s start by comparison of Δ OAP and Δ OBP:

From  the diagram, we can see that:

OA = OB (∵ radii of same circle)

∠ OAP = ∠ OBP = 90° (∵ tangent is to the radius)

PA = PB   (∵ tangents from the same point to a circle)

Now, by SAS identity of congruency, Δ OAP Δ OBP

Next, by CPCT rule, ∠ APO = ∠ BPO

Step 3: Next, we compare Δ QAP and Δ QBP:

Here, PA = PB   (∵ tangents from the same point to a circle)

∠ APQ = ∠ BPQ (∵ ∠ APO = ∠ BPO proved in step 2)

PQ = PQ  (∵ common arm)

Now, by SAS identity of congruency, Δ OAP Δ OBP

∴ by CPCT rule, we get (i) AQ = BQ    and (ii) ∠ AQP = ∠ BQP

Step 4: Let’s take both findings one by one:

Since AQ = BQ.

Therefore, OP is bisector of chord AB

Next, let’s take ∠ AQP = ∠ BQP

From the diagram, since ∠ AQP + ∠ BQP = 180⁰

and since ∠ AQP = ∠ BQP

∴ 2 ∠ AQP = 180⁰

∴ ∠ AQP = = 90⁰

Therefore, the line OP is perpendicular to AB.

Therefore, OP is perpendicular bisector to chord AB…………….. Hence Proved !

Please press the “Heart” button, if you like the solution.