Q) If AP and DQ are medians of triangles ABC and DEF respectively, where ∆ABC~ ∆DEF, then prove that 𝐴𝐵/𝐷𝐸 = 𝐴𝑃/𝐷𝑄.

[Q 23 – Sample Question Paper – CBSE Board 2026]

Ans: 

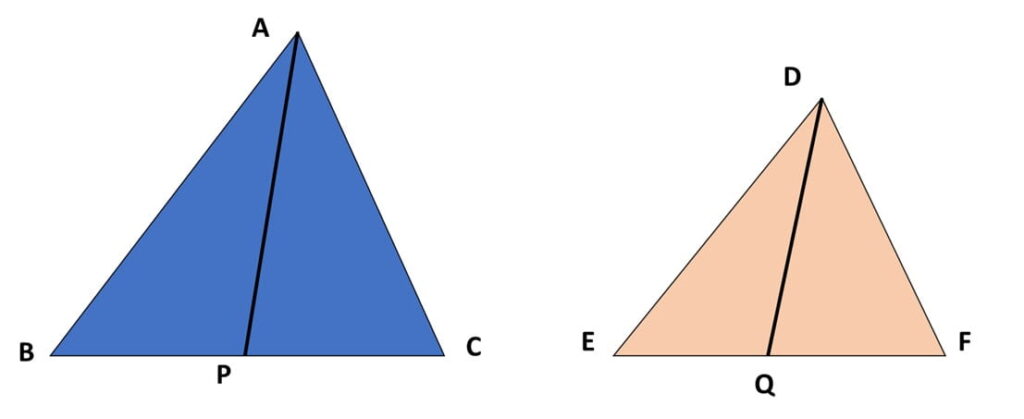
Step 1: Given that,  Δ ABC ~ Δ DEF, therefore

∠ B = ∠ E   …………. (i)

and …………. (ii)

Step 2: Since AP is median of BC, hence BC = 2 BP

Similarly, DQ is median of EF, hence EF = 2 EQ

Let’s substitute these 2 values in equation (ii), we get:

∴ …….. (iii)

Step 3: Let’s compare Δ ABP ~and Δ DEQ

Here,     (already proven in step 2)

∠ B = ∠ Q                      (identified in step 1)

∴ Δ ABP ~ Δ DEQ         (by SAS similarity)

Therefore,

Hence proved.

Please press the “Heart” button if you like the solution.