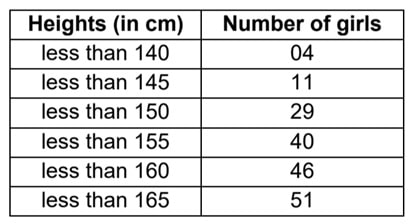
Q) A survey regarding heights (in cm) of 51 girls of class X of a school was conducted and the following data was obtained:

You can embed this directly into your HTML page. Want it styled with CSS or made responsive for mobile? I can help with that too!

Find the median height of girls. If mode of the above distribution is 148.05, find the mean using empirical formula.

Q35 B – Sample Question Paper – Set 1 – Maths Standard – CBSE 2026

Ans:

i. Median value of the given data:

Step 1: Let’s first normal the given data and group the girls according to the given heights:

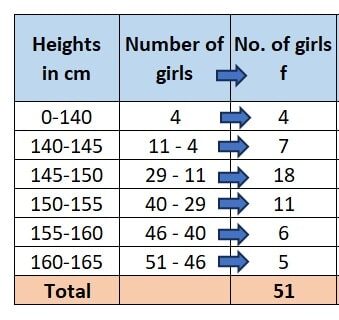
For 1st group, we take less than 140 and the count of girls in this group is 4  (given)

[Note: Ideally grouped data is taken as homogeneous set, hence 1st group can be 135 – 140. But since there is no additional information given and there can be girls less than 135 as well. Hence, we go ahead with “less than 140”]

2nd group we take 140 – 145 and the count of girls in this group will be: 11 – 4 = 7

3rd group we take 145 – 150 and the count of girls in this group will be: 29 – 11 = 18

4th group we take 150 – 155 and the count of girls in this group will be: 40 – 29 = 11

5th group we take 155 – 160 and the count of girls in this group will be: 46 – 40 = 6

6th group we take 160 – 165 and the count of girls in this group will be: 51 – 46 = 5

Step 2: let’s arrange these groups and the respective frequency f (= number of girls) in form a table:

Step 3: Next, we identify median class:

and to do this, we take calculate cumulative frequency, Σf, against each group.

Here, we get total of frequency = 51

We know that, Median class is the class where the cumulative frequency crosses 50% of total of frequencies.

Here, in the given data, total of frequencies is 51 and at row 3, cumulative frequency of 29 crosses 50% of total (i.e. 51/2 = 25.5)

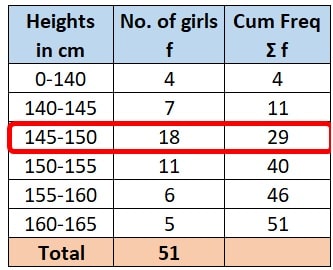
Hence, our Median class = 145 – 150

Step 4: Next, we calculate median value:

We know that the median value of a grouped data is given by: 

Median = L+ [ (n / 2 – c_f ) / f ] x h 

Here: 

L = Lower boundary of the median class = 145

n = Total number of frequencies = 51

c_f = Cumulative frequency of the class before the median class = 11

f = Frequency of the median class = 18

h = Class width = 150 -145 = 5

hence, the Median = 145 + [ (51 / 2 – 11 ) / 18 ] x 5

= 145 + [ (25.5 – 11 ) / 18 ] x 5

= 145 + (14.5  / 18 ) x 5

= 145 + (14.5  x 5  / 18 )

= 145 + 72.5 / 18

= 145 + 4.0277 = 149.03 cm

Therefore, the Median value of the given data is 149.03 cm

ii. Mean of given data:

We are given mode of the data = 148.05

We know, that according to empirical formula: 3 x Median = Mode + 2  x Mean

By substituting values of Median and Mode in above formula, we get:

3 x 149.03 = 148.05 + 2 x Mean

∴ 447.09 = 148.05 + 2 x Mean

∴ 2 x Mean = 447.09 – 148.05 = 299.04

∴ Mean = 299.04 / 2 = 149.52

Therefore, the mean value of data is 149.52

Please do press “Heart” button if you liked the solution