Q) Find the area of the major segment (in terms of 𝜋)  of a circle of radius 5 cm, formed by a chord subtending an angle of 90˚ at the centre.

[Q 24 B – Sample Question Paper – CBSE Board 2026]

Ans: 

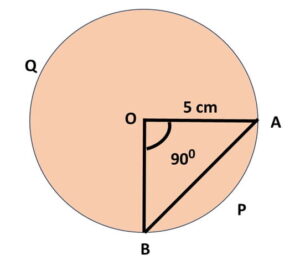
Let the chord AB cut the circle in 2 parts.

Sector APB is minor segment and AQB is major one.

Step 1: Now in △ AOB, radius OA = OB = 5 cm

Given that ∠AOB = 90°

Therefore, △ AOB, is a right angled triangle

∴ Area of △ AOB = (5)²   =  12.5 cm²

Step 2: Now, area of minor segment APB

= Area of sector OAPB – Area of △OAB

= π r²   − 12.5                      

=  x 5 x 5 x   − 12.5                        

= – 12.5

= 13.0952 – 12.5 = 0.595 cm²

Step 3: Now, Area of major segment AQB

= Area of circle – Area of minor segment APB

= π r² − Area of segment APB                       

= x 5 x 5 – 0.595

= 78.5714 – 0.595

= 78.52 cm²

Hence, the area of major segment of the circle is 78.52 cm².

Please click the “Heart” button, if you like the solution.