Q) From a solid cylinder of height 30 cm and radius 7 cm, a conical cavity of height 24 cm and same radius is hollowed out. Find the total surface area of the remaining solid.
Ans: Let’s draw the diagram to capture the shape:
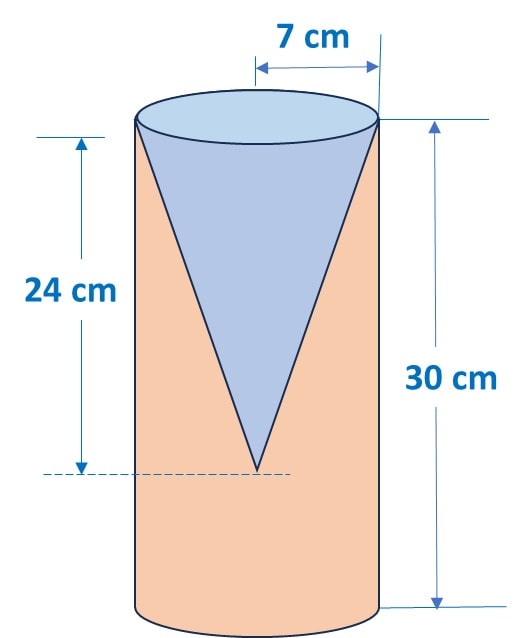
After taking out the conical shape from cylinder, total surface area of the remaining solid will be:
= Curved surface area of the cylinder + One side base area of the cylinder + Curved surface area of cone
(Note, here one side of the base is removed in the cavity)
= 2 ![]() r h +
r h + ![]() r2 +
r2 + ![]() r l
r l
= ![]() r (2 h + r + l ) …………. (i)
r (2 h + r + l ) …………. (i)
Here, it is given that height of the cylinder, h = 30 cm
radius of the cylinder, r = 7 cm
The slant height of the cone = ![]() = 25 cm
= 25 cm
By transferring these values in the equation (i), we get:
Total Surface area of the remaining solid = 7 ![]() [ 2 x 30 + 7 + 25]
[ 2 x 30 + 7 + 25]
= 644 ![]()
= (644) ![]()
= 2024 cm2
Therefore, the surface area of the remaining solid is 2024 cm2.
Please do press “Heart” button if you liked the solution.
