Q) Governing council of a local public development authority of Dehradun decided to build an adventurous playground on the top of a hill, which will have adequate space for parking.

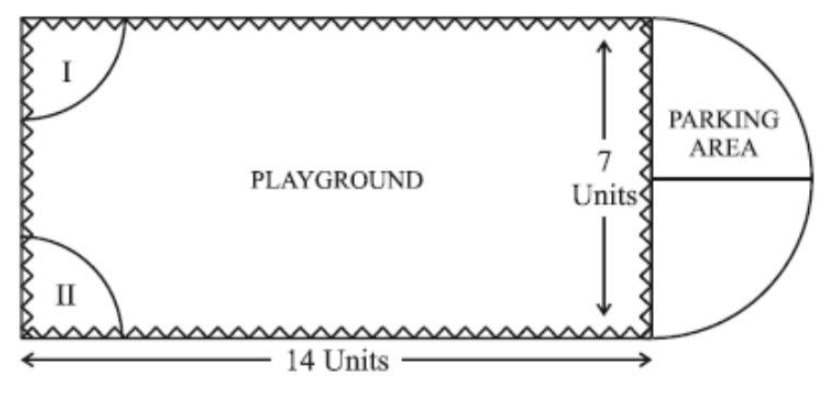
After survey, it was decided to build rectangular playground, with a semi-circular area allotted for parking at one end of the playground. The length and breadth of the rectangular playground are 14 units and
7 units, respectively. There are two quadrants of radius 2 units on one side for special seats.
Based on the above information, answer the following questions :
(i) What is the total perimeter of the parking area?
(ii) (a) What is the total area of parking and the two quadrants?
     OR
(b) What is the ratio of area of playground to the area of parking area?
(iii) Find the cost of fencing the playground and parking area at the rate of Rs. 2 per unit.

Ans: 

VIDEO SOLUTION

STEP BY STEP SOLUTION

(i) Perimeter of parking area = outer perimeter of semicircle + diagonal of semicircle

=

Given that, breadth or diameter of semicircle = 7 units

hence,

Therefore, Perimeter of parking area =

= 18 units

(ii)(a) Area of parking space and two quadrants = Area of Parking Space + Area of 2 quadrants

Since, both these type of areas have different radius, let’s consider that is the radius of parking space and is the radius of quadrant. We know that:

Since (calculated above)

and (given)

Area of parking space and two quadrants =

Total Area =

=  =

= 25.54 sq. units 

(ii) (b) Ratio of Playground area to Parking area =

=  =

= 56:11

(iii) Perimeter of required fencing = perimeter of playground + perimeter of parking area

= 2 (l + b) +

= 2(14+7) + x

= 42 + 11 = 53 units

Cost of fencing @ Rs. 2 per unit = 53 x 2

= Rs. 106

This completes all the required solutions.