Q) ) In the given figure, O is the centre of the circle and QPR is a tangent to it at P. Prove that ∠ QAP + ∠ APR = 90°.

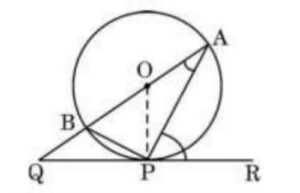
Ans:

VIDEO SOLUTION

STEP BY STEP SOLUTION

Since OA = OP (radii of same circle)

In Δ OAP,  ∠OPA = ∠ OAP .. (i)

Since tangent is perpendicular to radius

∠ OPR = 90⁰

∠ OPA + ∠ APR = 90°

Substituting values from equation (i), we get

∠ OAP + ∠ APR = 90°

Since ∠ OAP = ∠ QAP (by line AO extended till point Q)

∠ QAP + ∠ APR = 90°