Skip to content
Q: On a Sunday, your Parents took you to a fair. You could see lot of toys displayed, and you wanted them to buy a RUBIK’s cube and strawberry ice-cream for you. Observe the figures and answer the questions:-
1. The length of the diagonal if each edge measures 6cm is
a) 3√3. b) 3√6. c) √12. d) 6√3
2. Volume of the solid figure if the length of the edge is 7cm is
a)256 cm3. b) 196 cm3. c) 343 cm3. d) 434 cm3
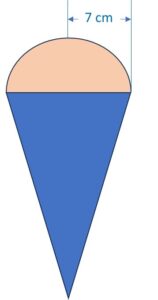
3. What is the curved surface area of hemisphere (ice cream) if the base radius is 7cm?
a) 309 cm2. b) 308 cm2. c) 803 cm2. d) 903 cm2
4. Slant height of a cone if the radius is 7cm and the height is 24 cm___
a) 26cm. b) 25 cm. c) 52 cm. d) 62cm
5. The total surface area of cone with hemispherical ice cream is
a) 858 cm2. b) 885 cm2. c) 588 cm2. d) 855 cm2
Ans:
1. Diagonal of the cube:
Let’s look the entire diagonal as combination of two right angled triangles.
In 1st right angled triangle, ABC, base BC and height AB are 6 cm each,
Therefore it’s diagonal, AC = 
Now, In the 2nd right angled triangle ACD, base AC is 
cm and height CD is 6 cm.
Therefore it’s diagonal, AD = 
cm
Alternate method:
Diagonal of a cube of 6 cm : 
= 
cm
Hence, option d) is correct option.
2. Volume of 7 cm cube:
Here solid figure is cube hence we will take cube as the solid figure.
Now, Volume of a cube is given by: (side)3
It is given that the length of the edge is 7cm,
Hence, volume of the cube = (7)3 = 343 cm3
Hence, option c) is correct option.
3. Curved surface area of hemispherical ice-cream:
The curved area of hemisphere = 
Here, given that base radius, 
cm
curved area of hemispherical icecream = 
= 2 x 22 x 7 = 308 cm2
Hence, option b) is correct option
4. Slant height of a cone:
From the adjoining figure:
Given that the Radius of the cone, 
= 7 cm
Height of the cone, 
= 24 cm
Now, from the adjoining figure:
= 25 cm
Therefore, slant height of the cone is 25 cm.
Hence, option b) is correct option.
5. Total surface area of cone with hemispherical ice cream:
Total surface area = curved surface area of conical base + curved surface area of hemispherical icecream
A) Surface area of conical base = π r l
Here, radius of cone, = 7 cm
Slant height of cone, = 25 cm (calculated in part 4)
Therefore, surface area of conical base = 
= 22 x 25 = 550 cm2
B) curved surface area of hemispherical icecream = 308 cm2 (calculated in part 3)
Therefore, Total surface area = 550 + 308 = 858 cm2
Hence, option a) is correct option.
Please do press “Heart” button if you liked the solution.