Q) The word ‘circus’ has the same root as ‘circle’. In a closed circular area, various entertainment acts including human skill and animal training are presented before the crowd.
A circus tent is cylindrical upto a height of 8 m and conical above it. The diameter of the base is 28 m and total height of tent is 18.5 m.

Based on the above, answer the following questions :
(i) Find slant height of the conical part.
(ii) Determine the floor area of the tent.
(iii) (a) Find area of the cloth used for making tent.
OR (iii) (b) Find total volume of air inside an empty tent.
Ans:
Let’s make a diagram fr the given question:
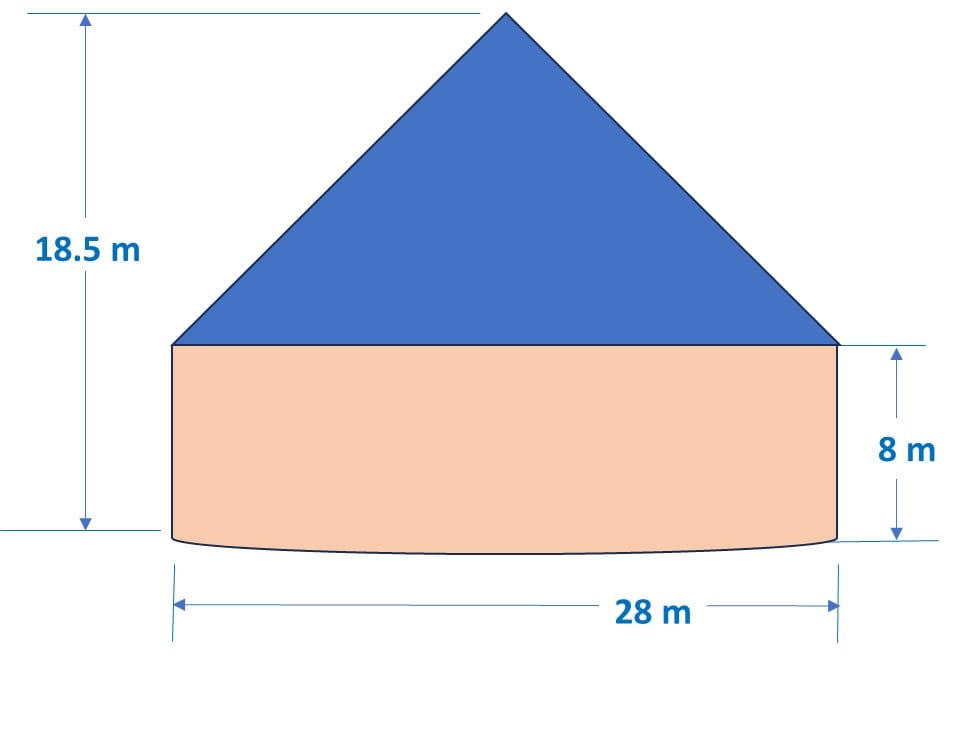
Here, in this question, it is given that:
Height of total shape = 18.5 m, height of cylindrical shape = 8 m,
Therefore, height of the canonical top = 18.5 – 8 = 10.5 m
Given that diameter of the base = 28 m
∴ Radius of the base = 14 m
(i) Slant height of the canonical top:
Slant height of the canonical top = √ [(14)2 + (10.5)2] = √ (306.25) = 17.5 m
Therefore, the slant height of the conical part is 17.5 m.
(ii) Floor Area of tent:
Floor area of tent = area of circle at the bottom = π R2
Since radius of the base circle = 14 m
∴ Floor area of tent = π R2
= ![]() = 22 x 14 x 2 = 308 x 2 = 616 m2
= 22 x 14 x 2 = 308 x 2 = 616 m2
Therefore, the floor area of the tent. is 616 m2
(iii)(a) Cloth are used for making tent:
Cloth required to make the tent = Curved surface area of conical part + curved surface area of cylindrical part
= π R L + 2 π R H = π R (L + 2 H)
Here, radius, R = 14 m, slant height L = 17.5 m, Height of cylinder, H = 8 m
Cloth required to make the tent = π R ( L + 2 H)
= ![]()
= 22 x 2 x (33.5) = 22 x 67 = 1474 m2
Therefore, 1474 m2 cloth will be required to make the tent
(iii)(b) volume of air inside empty tent:
Volume of air inside the tent = volume of conical part + volume of cylindrical part
= ![]()
= ![]()
Here, radius, R = 14 m, Height cone = 10.5 m, Height cylinder = 8 m
Volume of air = ![]()
= ![]() = 7,084 m3
= 7,084 m3
Therefore, volume of air inside the empty tent is 7,084 m3.
Please press the “Heart”, if you liked the solution.
