Q) A ball is thrown in the air so that t seconds after it is thrown, its height h metre above its starting point is given by the polynomial h = 25t – 5t2. Observe the graph of the polynomial and answer the following questions :
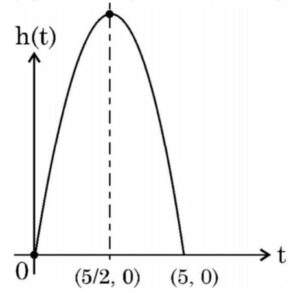
(i) Write zeroes of the given polynomial.
(ii) Find the maximum height achieved by ball.
(iii) (a) After throwing upward, how much time did the ball take to reach to the height of 30 m ?
OR (iii) (b) Find the two different values of t when the height of the ball was 20 m.
Ans:
STEP BY STEP SOLUTION
(i) Zeroes of the polynomial:
Given polynomial equation is h: 25 t – 5t 2 = 0
or – 5 t 2 + 25 t = 0
Let the roots of the polynomial be α and β.
We know that sum of roots (α + β) = ![]()
∴ α + β = ![]() = 5
= 5
Next, we know that the product of the roots (α x β) = ![]()
α . β = ![]() = 0
= 0
∴ α = 0, β = 5
(note: these are the values of t at which h becomes zero and the graph touches X-axis)
(ii) Maximum height by ball:
from the graph it is seen that the ball is achieving maximum height at t = ![]() sec
sec
Let’s calculate the value of h at t = ![]()
∵ h = 25 t – 5 t2
∴ h = 25 (![]() ) – 5 (
) – 5 (![]() )2
)2
= ![]() = 31.25 m
= 31.25 m
Therefore, the ball will achieve maximum height of 31.25 m
(iii) (a) Time taken to reach 30 m:
We are now given value of h = 30 m, and we need to find value of t
∴ 30 = 25 t – 5 t 2
∴ 5 t 2 – 25 t + 30 = 0
∴ t 2 – 5 t + 6 = 0 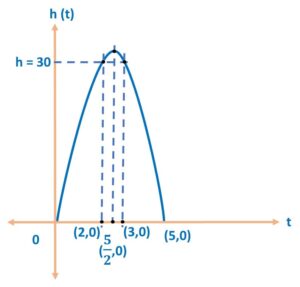
∴ t 2 – 3 t – 2 t + 6 = 0
∴ t (t – 3) – 2 (t – 3) = 0
∴ (t – 3) (t – 2) = 0
∴ t = 2 and t = 3
Therefore, that at both values of t = 2 and t = 3, the ball will be at 30 m height.
(Note: For your more clarity, we have plotted it in the graph as well.)
(iii) (b) time taken to reach 20 m:
We are now given value of h = 20 m, and we need to find value of t
∴ 20 = 25 t – 5 t 2
∴ 5 t 2 – 25 t + 20 = 0
∴ t 2 – 5 t + 4 = 0
∴ t 2 – 4 t – t + 4 = 0 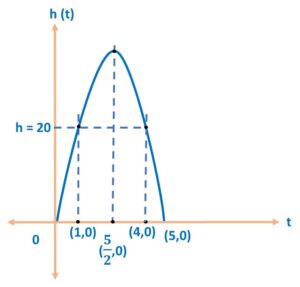
∴ t (t – 4) – (t – 4) = 0
∴ (t – 4) (t – 1) = 0
∴ t = 1 and t = 4
Therefore, that at both values of t = 1 and t = 4, the ball will be at 20 m height.
(Note: For your more clarity, we have plotted it in the graph as well.)
Please do press “Heart” button if you liked the solution.
